A Museum for Mathematics
| The Garden of Archimedes
A Museum for Mathematics |
The geometry of curves:
|
| |
| |
One of the properties of the straight line is that it is the shortest way between two points. So, if we want to cross a square, it's better to follow a straight line rather than another route.
 But if we want to go to New York, we will not be able to follow
a straight line, as the earth is round and there are no straight
lines on its surface. On a curved surface, geodetic curves take the place of straight lines. They represent the shortest possible way.
But if we want to go to New York, we will not be able to follow
a straight line, as the earth is round and there are no straight
lines on its surface. On a curved surface, geodetic curves take the place of straight lines. They represent the shortest possible way.
On a sphere, the geodetic curves are the maximum circles. This means that the circles have a plane passing through the centre of the sphere. If we want to go from A to B, we can imagine that A is a pole and then follow the meridian passing through B.
The Polar routes satisfy the need to cover the shortest possible path, to save time and fuel. To travel between two cities at the same latitude, rather than following the parallel, it is better to deviate towards the pole.
The geodetic curves of a surface can be found by solving a differential equation, involving the metrical system of the surface. This is the way to measure distances between close points, a metrical system that varies from one surface to another. Sometimes different equations can be used on the same surface. For example, while the usual distances can be measured on a straight line (as the crow flies), in the case of a mountain it is preferable to measure in hours of journey, therefore distances on a slope are longer than on a plain.
An interesting distance is the metrical system of Poincaré (Henri Poincaré, 1854-1912). Imagine moving on a semiplane delimited by a line, the horizon, and filled by a liquid that gets stickier as one gets closer to the horizon. Increasing amounts of time are needed to cover the same distance as one advances. The distance of Poincaré, between two points, is the time it takes to go from one to the other. In this universe, the distance between two vertical lines increases as we move towards the horizon. It is impossible to reach this line - the horizon is infinitely distant.
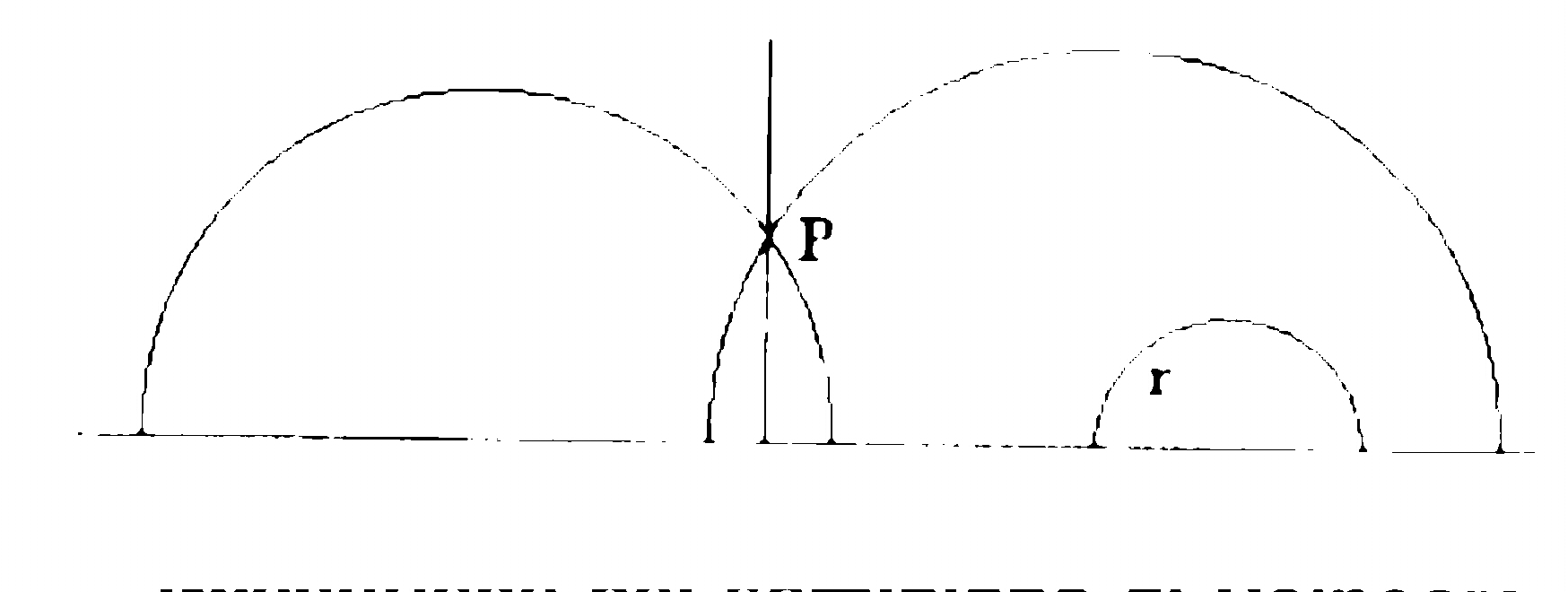 The shortest way between two points is a straight line,but only if
the two points are on the same vertical - otherwise it is best to
avoid the "sticky space". Geodetic curves, taking the place of lines,
are the circumferences whose centre is on the horizon.
The shortest way between two points is a straight line,but only if
the two points are on the same vertical - otherwise it is best to
avoid the "sticky space". Geodetic curves, taking the place of lines,
are the circumferences whose centre is on the horizon.
In the semiplane of Poincaré the postulate of the parallels does not apply. There are infinite parallels to a given line passing through a point.
Geodetic curves have particular importance in general relativity. One of Einstein's maxims is that space becomes curved near of celestial bodies. Consequently, a ray of light passing near the sun moves along a geodetic curve, which is significantly different to a straight line. The deviation of the light rays - observed during the eclipse of the sun - is one of the experimental proofs of general relativity.