I problemi classici   

Pur contenendo segni di lontane origini pratiche, gli Elementi euclidei sono un'opera matura, nella quale la struttura assiomatico-deduttiva è compiutamente sviluppata, anche se non totalmente rigorosa. La loro varietà mostra i sedimenti di generazioni di geometri, che dalle pratiche apprese dagli Egizi hanno saputo creare una scienza totalmente nuova per impianto teorico, e di una ricchezza che i tenditori di corde e tracciatori di cerchi non avrebbero potuto nemmeno immaginare.

Nondimeno, alcuni problemi rimangono ostinatamente fuori dal dominio della retta e del cerchio, ormai diventato il mondo di carta della riga e del compasso. Tra questi, i tre problemi classici: la duplicazione del cubo, la trisezione dell'angolo, la quadratura del cerchio.

Narra la leggenda che, essendo la Grecia funestata da una tremenda epidemia, una delegazione si recò presso l'oracolo di Delo per chiederne la fine. La risposta dell'oracolo fu che l'ira degli dei si sarebbe placata qualora l'altare a essi dedicato, a forma di cubo, fosse stato sostituito con uno della stessa forma, ma grande il doppio. I messi, solerti ma poco saggi, fecero immediatamente costruire un altare, sempre a forma di cubo, e con il lato doppio del primo. Poiché la pestilenza non accennava a calmarsi, si consultò di nuovo l'oracolo, e si scoprì che il nuovo altare non era grande il doppio, ma otto volte più del primo. Infatti, essendo uguale ad a³ il volume del cubo di lato a, quello di lato 2a avrà volume (2a)³. Se invece si vuole raddoppiare il cubo di lato a, bisogna costruirne uno di lato 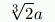, in modo che il suo volume sia .

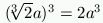Se si dimentica la leggenda, e ci si pone da un punto di vista esclusivamente geometrico, il problema consiste, dato un segmento di lunghezza a, nel costruire un secondo segmento, di lunghezza 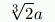. Ora, mentre è facile costruire con riga e compasso un segmento lungo 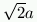(basterà costruire un quadrato di lato a, la cui diagonale è lunga 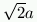), e quindi raddoppiare un quadrato (si prende il quadrato costruito sulla diagonale del primo), raddoppiare un cubo non è altrettanto facile. Al contrario, si è dimostrato, anche se in tempi relativamente moderni, che il problema non è risolubile usando esclusivamente la riga e il compasso: il problema di Delo richiede l'uso di strumenti e tecniche più complessi.

Lo stesso accade per gli altri problemi. Per questi, i geometri inventano nuove curve, spingendosi al di là dei limiti delle rette e dei cerchi: Ippia di Elide (V sec. a. C.) inventa la quadratrice, una curva per mezzo della quale egli ottiene la quadratura del cerchio, come pure la trisezione dell'angolo.

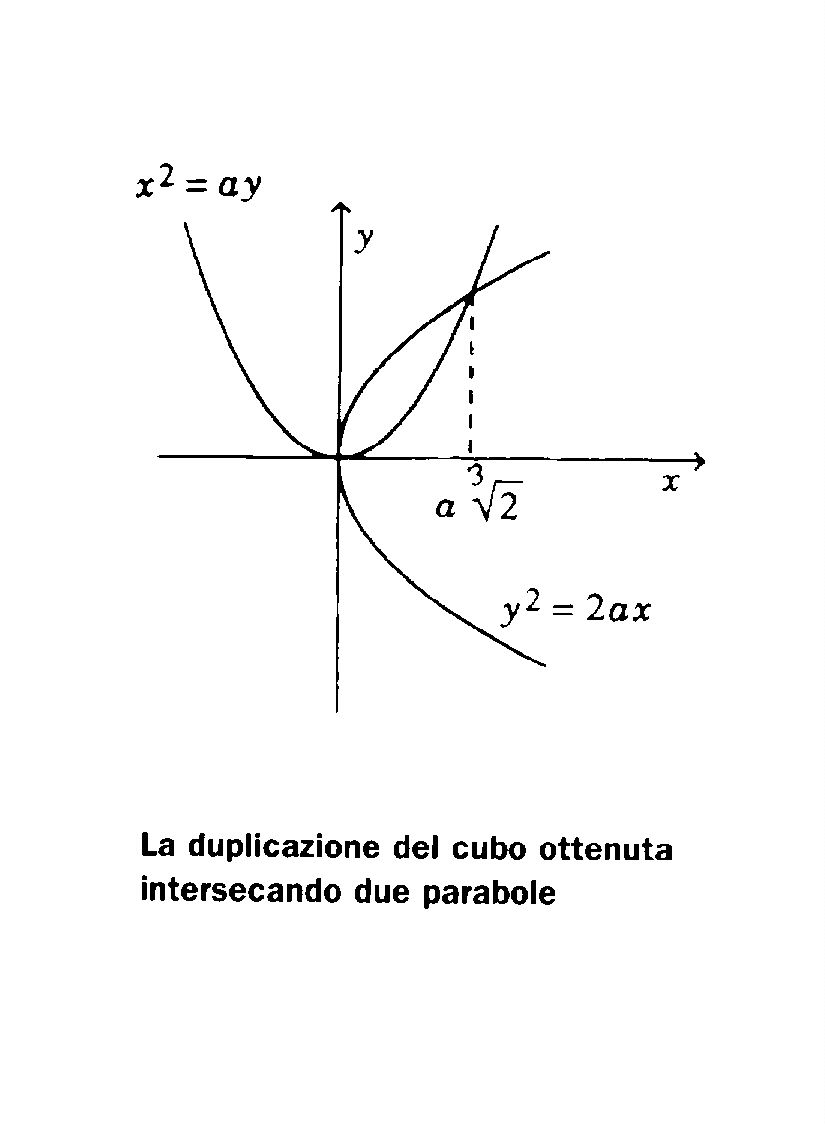Più tardi, il problema della duplicazione del cubo è risolto da Archita di Taranto (o forse da Menecmo di Proconneso, ambedue vissuti attorno al 400 a. C.) per mezzo dell'intersezione di due parabole, e da Diocle (II sec. a. C.) tramite una nuova curva, la cissoide. Il metodo di Archita è molto ingegnoso, e facile da descrivere usando le notazioni moderne della geometria cartesiana. Si considerino due parabole, di equazioni y² = 2ax e x² = ay. Se il punto di coordinate (x,y) appartiene ad ambedue queste curve, si avrà x⁴ = a²y² =2a³x, da cui, trascurando la soluzione x=0, si trova x³=2a³, e quindi 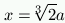. In definitiva, intersecando le due parabole si ottiene un punto la cui ascissa è il lato del cubo doppio.

Naturalmente, abbiamo molto semplificato la descrizione del procedimento di Archita, che in particolare, non conoscendo la geometria cartesiana e in particolare l'uso delle coordinate, si serviva di metodi e risultati esclusivamente geometrici. Quello che è più interessante è che nella dimostrazione entrano per la prima volta delle curve che saranno oggetto di studio per molti secoli a venire: le sezioni coniche.