La via più breve   

Una delle proprietà della retta è di essere la linea più breve tra due punti. Così, se vogliamo attraversare una piazza, sarà più conveniente muoversi in linea retta piuttosto che seguire un qualsiasi altro cammino.

Se però vogliamo andare a New York, non potremo seguire una linea retta, dato che la terra è rotonda e sulla sua superficie non ci sono linee rette. Su una superficie curva, il posto delle rette viene preso dalle curve geodetiche, lungo le quali il percorso è il più breve possibile.

Sulla sfera, le geodetiche sono i cerchi massimi, cioè i cerchi il cui piano passa per il centro della sfera. Se vogliamo andare da A a B, possiamo immaginare che A sia un polo e seguire il meridiano che passa per B.

Le rotte polari rispondono all'esigenza di percorrere il minor cammino possibile, in modo da risparmiare tempo e carburante. Per viaggiare tra due città alla stessa latitudine, non conviene seguire un parallelo, ma piuttosto deviare verso il polo.

Le geodetiche di una superficie si possono trovare risolvendo un'equazione differenziale, che coinvolge la metrica della superficie, cioè il modo di misurare le distanze di punti vicini. Questa metrica varia da una superficie a un'altra, e talvolta si possono usare metriche diverse sulla stessa superficie. Ad esempio, mentre le distanze usuali si misurano in linea d'aria, in montagna si preferisce misurare in ore di cammino, per cui le distanze in salita risultano più lunghe di quelle in piano.

Una distanza interessante è la metrica di Poincaré (Henri Poincaré, 1854-1912). Immaginiamo di muoverci in un semipiano delimitato da una retta, l'orizzonte, e riempito da un liquido che diviene sempre più vischioso man mano che ci si avvicina all'orizzonte, in modo che per percorrere lo stesso spazio occorra un tempo sempre maggiore, inversamente proporzionale alla distanza dall'orizzonte. La distanza di Poincaré tra due punti è il tempo impiegato per andare da uno all'altro. In questo universo, la distanza tra due rette verticali va aumentando via via che ci si muove verso l'orizzonte. A questa retta non si arriva mai: l'orizzonte è a distanza infinita.

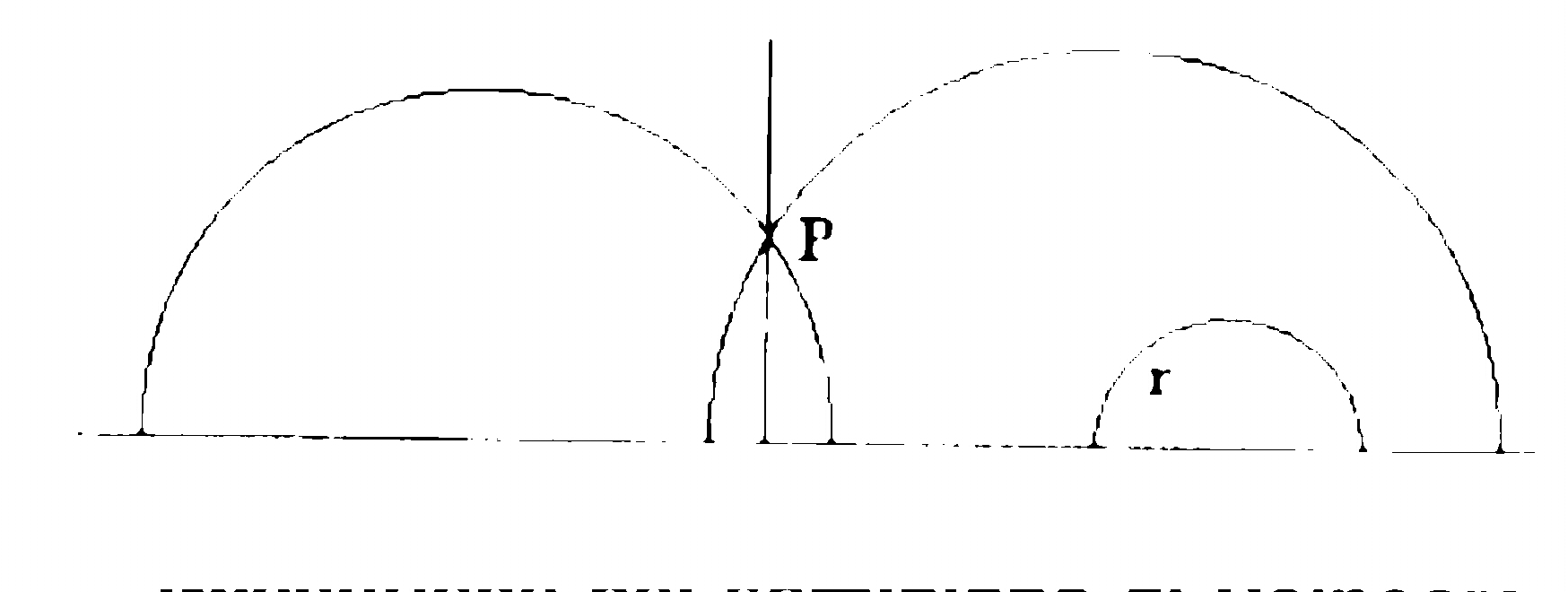Il cammino più breve tra due punti è una retta, solo se i due punti stanno sulla stessa verticale; altrimenti conviene allontanarsi dalla zona vischiosa. Le geodetiche, che prendono il posto delle rette, sono le circonferenze con centro sull'orizzonte.

Nel semipiano di Poincaré non vale il postulato delle parallele: per un punto pasano infinite parallele a una retta data.

Le geodetiche rivestono un'importanza particolare in relatività generale. Una delle intuizioni di Einstein è che lo spazio si incurvi nelle vicinanze dei corpi celesti. Di conseguenza, un raggio di luce che passi nelle vicinanze del sole, si muoverà lungo una geodetica sensibilmente diversa da una retta. La deviazione dei raggi luminosi, osservata durante le eclissi di sole, è una delle conferme sperimentali della relatività generale.