Nella vita quotidiana ci si imbatte spesso in meccanismi di svariati tipi costituiti da aste rigide tra loro incernierate oppure scorrevoli l'una sull'altra.

Si pensi ai semplici congegni per aprire porte o finestre, ai freni delle biciclette, alle spillatrici, alle bilance, alle macchine da scrivere, ai tecnigrafi o agli innumerevoli congegni di una automobile: le sospensioni, le bielle del motore, il tergicristallo, lo sterzo, il carburatore, per non citare che un piccolo campionario di ciò che incontriamo tutti i giorni a casa o sul luogo di lavoro. D'altra parte anche la struttura stessa del corpo umano e dei vertebrati in generale è costituita da ossa (le aste) e articolazioni (le cerniere).

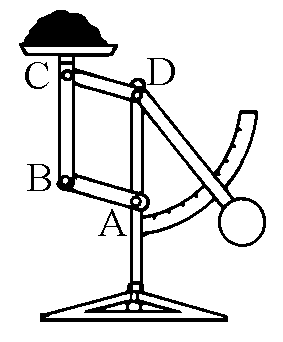
Semplici meccanismi, costituiti da elementi rigidi incernierati o scorrevoli, hanno consentito la costruzione di macchine che trasmettono o amplificano la forza umana o animale, oppure forze naturali (come quelle prodotte dall'acqua o dal vento) o artificiali (vapore, elettricità), consentendo di compiere operazioni predeterminate con risparmio di fatica e di tempo e con caratteristiche di uniformità e precisione. Ed è proprio l'uso intensivo e generalizzato di questi meccanismi che ha determinato lo sviluppo della produzione industriale, con l'impiego di macchine a loro volta prodotte da altre macchine.

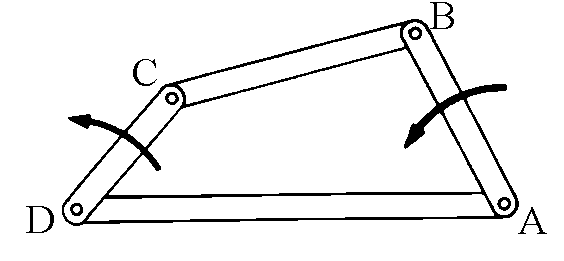
Cosa hanno in comune tutti questi meccanismi semplici o complessi? Tanto per cominciare ciascuno di essi coinvolge parti in movimento, tali parti interagiscono fra di loro in modo da convertire un tipo di movimento in un altro. Ad esempio nel semplice meccanismo di una serratura, girando la chiave in un verso o nell'altro il chiavistello fuoriesce o rientra nella sua sede: un movimento rotatorio viene trasformato in un movimento traslatorio.

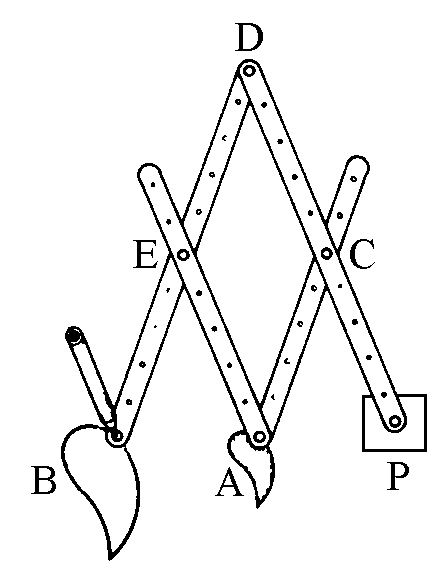
Durante il movimento, i punti chiave del meccanismo, vale a dire i perni o gli scorrevoli, descrivono delle curve che sono più o meno complesse a seconda delle funzioni svolte. Si pensi al pantografo: se P è fissato e il punto A descrive una curva allora il punto B descrive un'altra curva che ha la stessa forma della prima ma è ingrandita due volte. Variando la lunghezza delle aste si può far sì che la nuova curva sia ingrandita o rimpicciolita di un fattore diverso rispetto alla prima. Il meccanismo trasforma una curva in un'altra curva.

A ben pensarci, questo fatto è vero per tutti i meccanismi, anche quelli che non sono costruiti per disegnare curve, anche quelli il cui funzionamento non appare, a prima vista, minimamente legato ad alcuna curva. Se un punto del meccanismo segue un percorso "semplice" allora un altro punto può descrivere un percorso molto più complesso o difficile da ottenere direttamente, sì che vien voglia di dire che un meccanismo è un congegno che trasforma una curva in un'altra. L'interesse e l'importanza di questi biellismi, meccanismi, congegni articolati, o come altro li vogliamo chiamare, consiste proprio nel fatto che essi fanno in modo che un dato loro punto si muova lungo una curva opportuna senza che il profilo di quest'ultima sia materialmente presente. D'altra parte la stessa agilità e versatilità della nostra mano, da cui deriva in parte la nostra creatività, dipende da un complesso meccanismo articolato tramite il quale non solo riusciamo con una matita a tracciare una curva o una figura che è presente solo nella nostra immaginazione mentre non è affatto intrinseca nelle articolazioni, ma riusciamo a girare una chiave, a stringere una pinza, a far descrivere a una racchetta da tennis una determinata traiettoria.