Che il problema del moto rettilineo fosse considerato molto importante in quel periodo è dimostrato dai piu' di 150 articoli apparsi nel diciannovesimo secolo su questo argomento in riviste di meccanica, ma anche di matematica. Un matematico di grande valore, il russo Tchebycheff, cui si devono fondamentali risultati nella teoria della probabilità e nella teoria dei numeri, dedicò molte energie per trovare una soluzione "esatta" del problema. Nel 1850 Tchebycheff riuscì a determinare un'altra soluzione approssimata al problema, forse più accurata di quella di Watt ma certamente meno pratica. Essa si basa su un biellismo a tre aste DA, AB, BC con C, D fissati, BC = AD e con le distanze coinvolte tali che AD : CD : AB = 5 : 4 : 2 . Attorno alla posizione simmetrica mostrata nella figura 4,  il punto medio P di AB descrive un percorso sostanzialmente rettilineo (anche se la traiettoria completa di P assomiglia a un semicerchio!). Sylvester scrive che, dopo gli sforzi intrapresi invano, Tchebycheff era pervenuto alla convinzione che non vi fosse alcun meccanismo in grado di dare una risoluzione esatta del problema.
Il meccanismo di Tchebycheff venne usato per guidare il moto delle lame di seghe per tagliare tronchi.
Toccò a un allievo di Tchebycheff, Lipkin, trovare il meccanismo che risolve in modo esatto il problema, in questo preceduto da Peaucellier, un ufficiale dell'esercito francese di cui diremo tra breve.

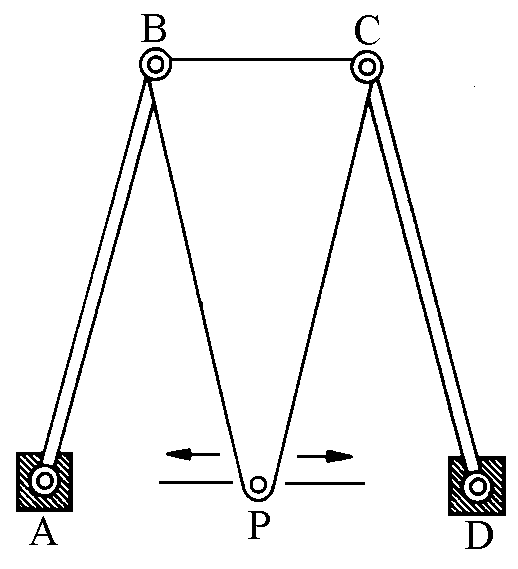
Nel frattempo l'inglese Roberts aveva proposto un'altra soluzione approssimata, basata su un biellismo a tre aste e su una lamina BPC a forma di triangolo isoscele. In questo caso si deve avere AB = BP = PC = CD e AD = 2 ·BC , il vertice P della lamina descrive per un tratto considerevole un percorso quasi rettilineo.