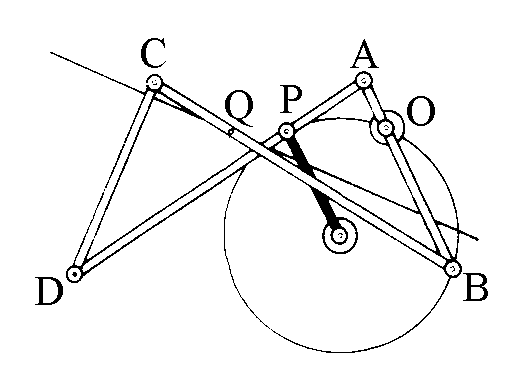
Un altro biellismo che risolve il problema del moto rettilineo è stato descritto da Hart; nel 1874, esso è basato su un "parallelogramma intrecciato" rappresentato a lato, ove AB = CD, AD = BC .
Se O, P, Q sono tre punti fissi sulle aste AB, AD, BC allineati in modo che la retta sulla quale giacciono sia parallela ad AC, lo stesso avverrà in qualsiasi posizione del biellismo e si ha OP · OQ = BQ · QC - OA · OB = costante. Pertanto se O è fisso i punti P e Q si corrispondono in una inversione circolare e, se P si muove su una circonferenza passante per O, il punto Q descrive una retta.

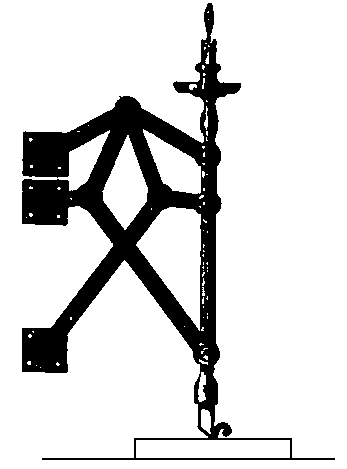
Con il meccanismo di Hart lo studio dei biellismi per il movimento rettilineo ha raggiunto la minima complessità: si può infatti dimostrare che con meno di cinque aste non è possibile risolvere il problema. Ma molti altri meccanismi sono stati inventati allo scopo, ad esempio quello mostrato a lato, basato su due doppi aquiloni, si riesce a traslare il supporto di una candela mantenendolo verticale.