|
Curve e meccanismi
F. Conti
(dal catalogo della mostra)
Cosa è un meccanismo?
Il problema del moto rettilineo senza parti striscianti
Il meccanismo di Watt
Il meccanismo di Tchebycheff
L'inversore di Peaucellier
Il biellismo di Hart
Curve, biellismi e profili
Il quadrilatero articolato e alcune applicazioni
|
|
Curve, biellismi e profili
|
|
Curve algebriche e biellismi
Nel 1875 Kempe ha dimostrato che qualsiasi curva algebrica può venir
tracciata con un biellismo. Ma anche per una curva semplice come una conica il meccanismo
può essere molto complicato.
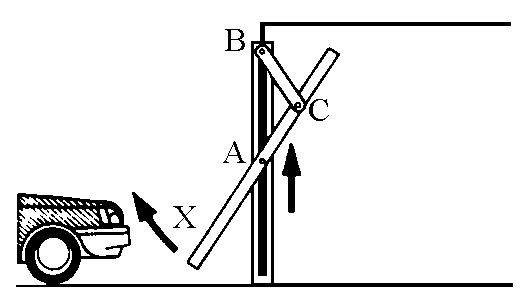
Nel movimento di una porta basculante, come sono quelle di molte
autorimesse, il punto X descrive una ellisse, ma sarebbe
fuor di luogo sostenere che il meccanismo è stato realizzato per questo.
|
|
|
Profili e curve
Al contrario capita talvolta in tecnologia che sia il profilo
di una certa curva a determinare le funzioni di un meccanismo. E' il caso di
tutti i congegni basati su sistemi a camma e punteria.
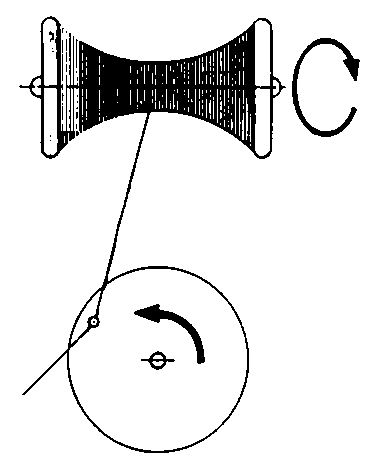
Basti un solo esempio: per avvolgere un filo in modo uniforme su un
rocchetto occorre che la guida che indirizza il filo si muova con velocità costante
(alternativamente da destra a sinistra e da sinistra a destra). Se si usufruisse del più
semplice meccanismo ipotizzabile, con una guida del filo
che si muove di moto circolare uniforme, la proiezione di detta guida sull'asse del
rocchetto (cioè la posizione del filo che si avvolge) si muoverebbe di moto armonico,
depositando molto più filo alle estremità che non al centro.
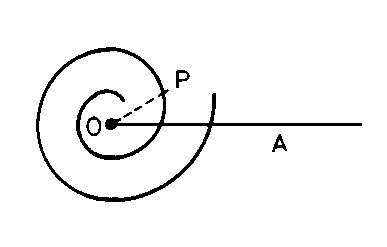
Una soluzione al problema si ottiene usando la spirale di Archimede. Questa è una curva i cui punti P hanno la seguente
proprietà: la loro distanza da un punto fisso O cresce proporzionalmente all'angolo
formato dal segmento PO con una fissata semiretta OA di riferimento. E' una curva che si
incontra sovente in oggetti di uso quotidiano (i nastri magnetici, i rotoli di fune, le
decorazioni di certi dolci,...).
Usando una camma formata da due "spezzoni" della spirale di
Archimede si riesce facilmente a risolvere il problema di avvolgere il filo uniformemente. Questa è la soluzione universalmente adottata nelle
macchine da cucire per avvolgere la "bobina".
|


|
|
|