|
Curve e meccanismi
F. Conti
(dal catalogo della mostra)
Cosa è un meccanismo?
Il problema del moto rettilineo senza parti striscianti
Il meccanismo di Watt
Il meccanismo di Tchebycheff
L'inversore di Peaucellier
Il biellismo di Hart
Curve, biellismi e profili
Il quadrilatero articolato e alcune applicazioni
|
|
Il quadrilatero articolato e alcune applicazioni
|
|
Come si è visto, semplici meccanismi di aste incernierate risolvono
problemi che hanno notevole interesse sia teorico che pratico. Il più semplice di questi
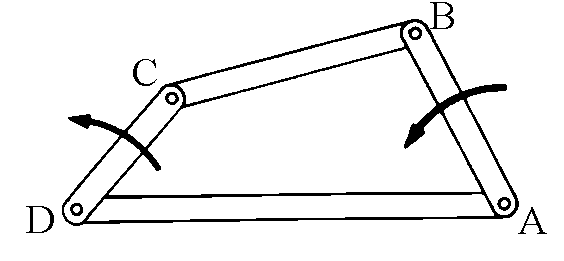
meccanismi è il quadrilatero articolato. Se si considera il quadrilatero ABCD
con un lato AD fissato, è chiaro che la posizione di una delle tre aste determina quella
delle rimanenti. Si tratta di un meccanismo a un solo grado di libertà.
Nella versione mostrata nella figura a lato, se si
ruota l'asta CD di moto antiorario, anche l'asta AB inizia a girare in senso antiorario;
ad un certo punto però quest'ultima inverte la direzione del moto, pur continuando CD
nella sua rotazione antioraria. Non è facile immaginare il movimento di questo semplice
congegno, converrà realizzare un semplice modello con strisce di cartone o aste di
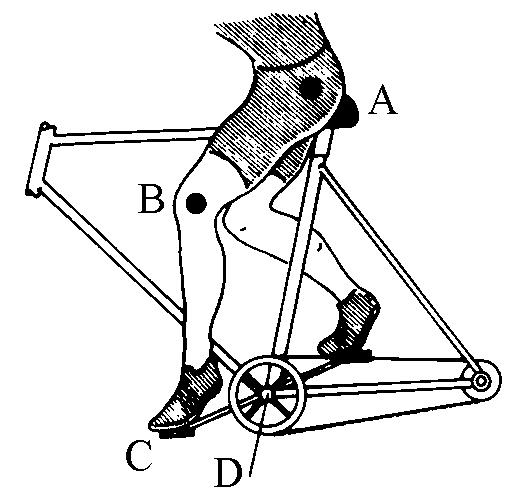
Meccano o altro, oppure guardare la figura accanto: la gamba della
ciclista e il braccio del pedale formano un quadrilatero articolato del tutto simile a
questo.
Questa difficoltà nel prevedere il tipo di movimento dipende anche dal
fatto che, variando il rapporto fra le lunghezze delle aste, il funzionamento del sistema
può essere molto diverso, e in questo sta il fascino, l'interesse e l'utilità del
quadrilatero articolato.
|
|
|
Se le aste opposte sono di egual lunghezza il sistema diviene un parallelogramma
articolato e tali coppie di aste rimangono sempre parallele fra loro. Questo fatto è
alla base di numerosissime applicazioni del meccanismo che sono quotidianamente sotto i
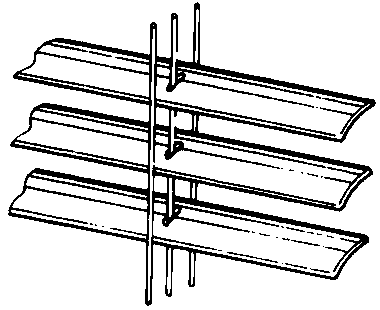
nostri occhi. I tecnigrafi, le bilance, le tende
alla veneziana, i tergicristalli degli autobus (anche quelli delle automobili, ma in
questo caso il meccanismo è più nascosto) utilizzano questo semplice meccanismo. Esso si
trova ancora in certe lampade da tavolo, nei sollevatori,
nei cambi delle biciclette, nei cestini da cucito . . .
In tutti i casi in cui è fondamentale che certe parti mantengano una giacitura prefissata
il parallelogrammo articolato fornisce la soluzione adeguata. Ad esempio nel caso dei
sollevatori per l'ispezione dei lampioni stradali occorre garantire che la base della
cabina rimanga ben orizzontale qualunque sia l'altezza dal suolo. Si noti che in alcuni
degli esempi descritti si utilizzano due parallelogrammi accoppiati, in questo modo si
possono ottenere movimenti in due direzioni (si hanno due gradi di libertà) ma il
parallelismo del movimento è sempre garantito.
|
|
|
Lo
stesso pantografo è basato
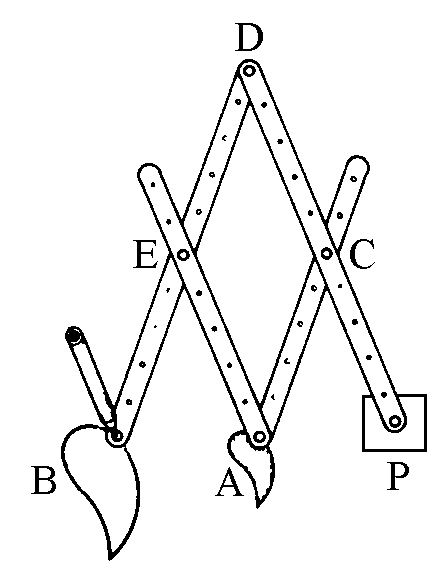
sostanzialmente su un doppio parallelogramma articolato (nel caso della figura 1 si tratta
di un rombo). Se
PC = CD = DE = EB = AE = AC allora i
punti P, A, B sono sempre allineati e la distanza di B dal punto fisso P è sempre il
doppio di quella di A, dunque, se A descrive una curva, B descrive una curva simile
ingrandita di un fattore due.
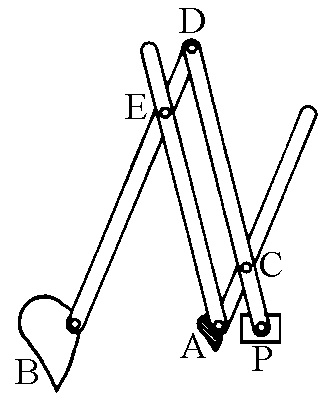
La figura a lato mostra lo schema di un pantografo
nella configurazione per la quale il fattore di ingrandimento è quattro.
Nel caso generale, come si è detto, il quadrilatero articolato ha
funzionamento diversificato a seconda dei rapporti fra le lunghezze delle aste. Non è
questa la sede per una analisi dettagliata delle varie tipologie assunte, cercheremo solo
di mettere in evidenza la grande versatilità di questo meccanismo. Sovente esso è usato
come moltiplicatore di sforzo, nei casi in cui il movimento è impartito da un albero
ruotante a velocità quasi costante, mentre lo sforzo deve essere applicato solo in un
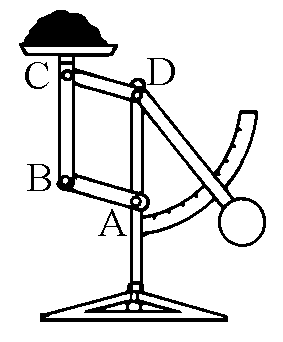
breve tratto con piccoli spostamenti, come avviene nei frantoi o in certe taglierine. O viceversa troviamo questo meccanismo con la funzione di
trasformare il moto alternato in moto circolare, come avviene nel pedale delle vecchie
macchine da cucire o con funzioni ancora più
nascoste, come avviene nei secchi della spazzatura.
|
|
|
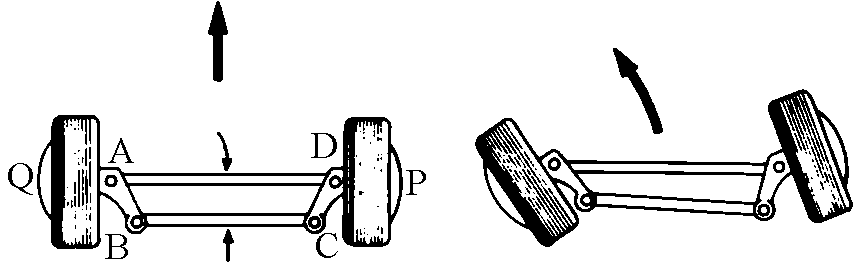
Interessante
è l'uso del quadrilatero articolato nel progetto delle
sospensioni di un autoveicolo (figura) studiato in modo da
consentire alle ruote di assorbire gli urti dovuti alle asperità della strada senza
trasmetterli direttamente all'abitacolo. In questo caso occorre far sì che l'angolazione
delle ruote rispetto alla verticale rimanga la stessa per entrambe le ruote.

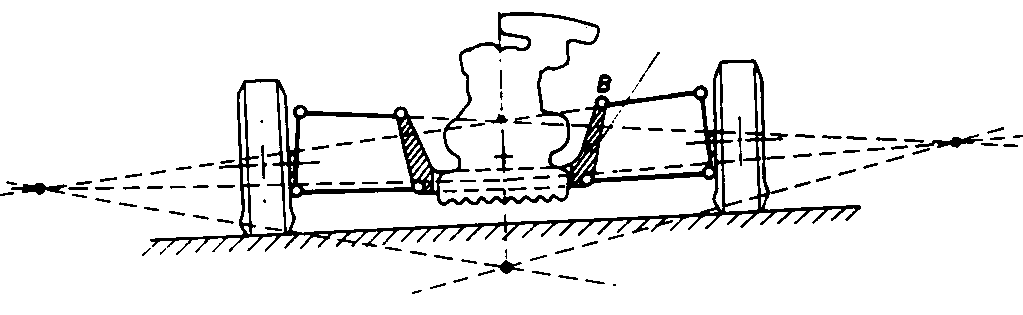
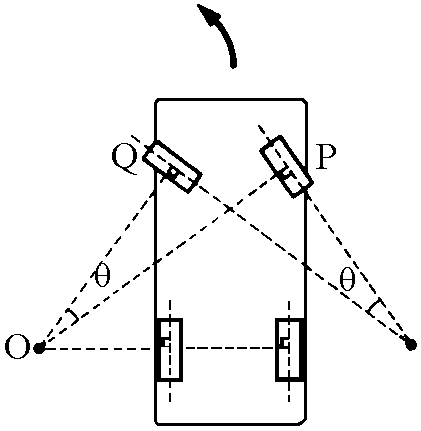
Ancora più interessante è l'uso del quadrilatero articolato nello
sterzo delle vetture. Il problema in questo caso è quello di consentire alle ruote di un
veicolo di avere, in curva, assi che passano per un medesimo punto, qualunque sia il
raggio di sterzata. Se non si rispetta questa condizione il veicolo perde stabilità in
curva e i pneumatici vengono sollecitati con forze trasversali usurandosi rapidamente. La
soluzione è stata trovata dall'ingegnere tedesco Ackermann nel 1818 e applicata alle
carrozze. Successivamente perfezionata da Jantaud e da Panhard, essa è descritta nella figura ed è basata su un trapezio articolato.

|
|
|
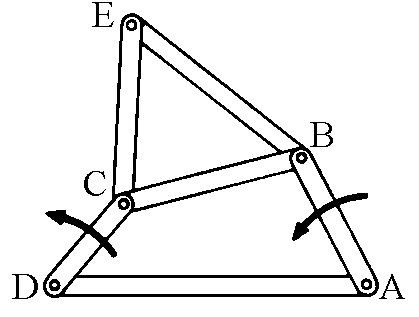
Se si considera
un piano solidale con l'asta CB allora mantenendo sempre AD fissato e ruotando l'asta più
corta i punti di questo piano descrivono delle curve molto diverse tra loro, a seconda
della posizione del punto. Per individuare il punto tracciante del piano vincolato
all'asta BC basta aggiungere al meccanismo altre due aste BE, CE che formano un triangolo
con BC.
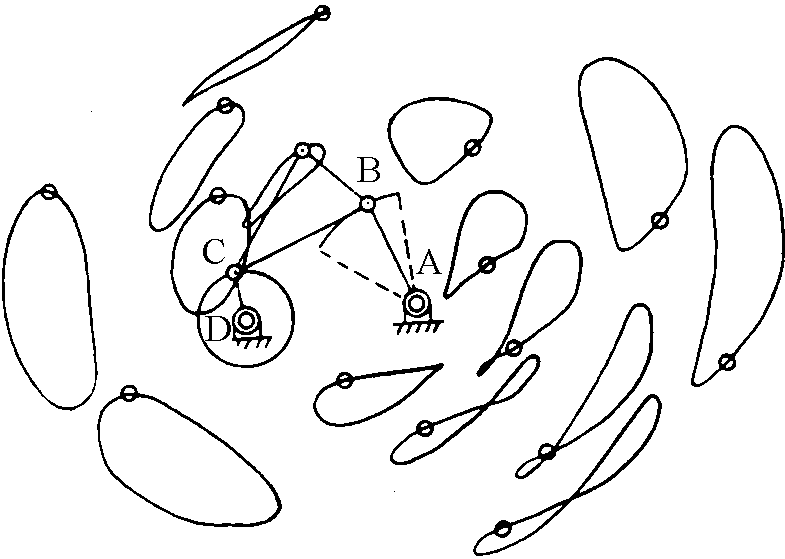
La figura successiva dà un'idea di questo fenomeno,
alcune di queste curve hanno la forma di un 8 allungato, altre sono ovoidali, altre ancora
hanno un tratto quasi rettilineo.

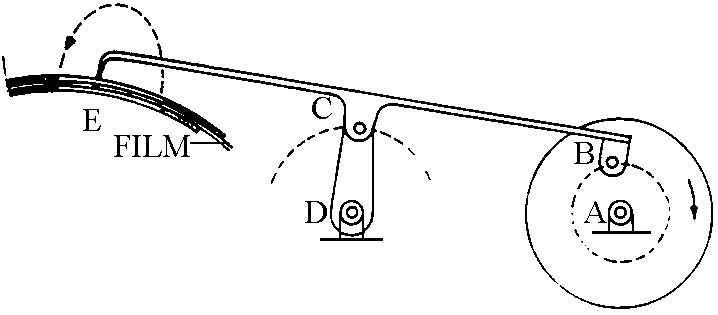
Quest'ultima opportunità viene sfruttata ad esempio nel meccanismo di
trascinamento della pellicola nei proiettori e nelle cineprese (figura). Quando B compie una
rivoluzione completa attorno all'asse A, la punta E percorre la traiettoria tratteggiata, determinando l'avanzamento repentino della pellicola
nel tratto quasi rettilineo per poi disimpegnarsi e riposizionarsi nell'altra parte di
traiettoria.

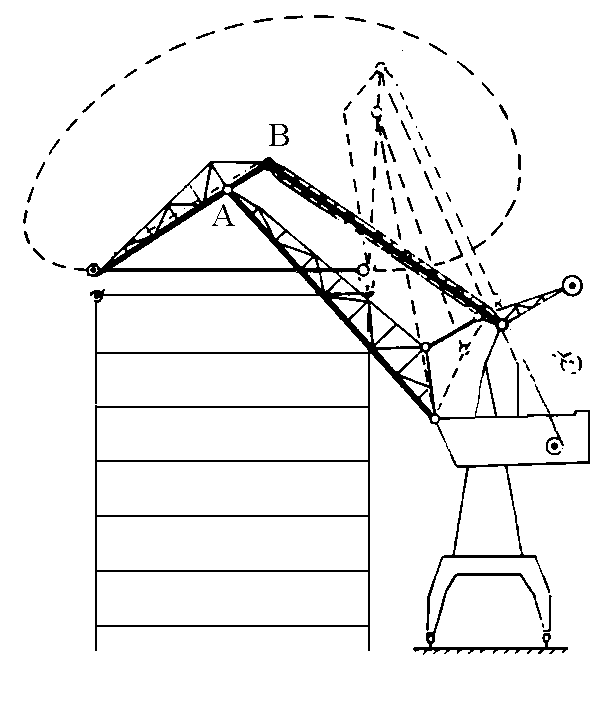
Anche il progetto dei bracci di una gru approfitta di questa proprietà in questo caso il problema è quello di fare in modo
che variando la distanza dalla base l'altezza del carico rimanga quasi inalterata.
Ovviamente funzioni ancora più complesse possono essere svolte da
meccanismi più complessi, ma il problema non è in linea di principio dissimile dai casi
semplici che abbiamo analizzato; ciò che si vuole ottenere da un congegno è che un dato
punto descriva una determinata traiettoria che stabilisce il suo funzionamento, senza che
questa traiettoria sia fisicamente presente.
Come ricordato, Kempe ha dimostrato che esiste un biellismo che traccia
ogni curva algebrica; tuttavia in generale tale meccanismo è costituito da un numero
molto grande di aste. L'aver determinato di volta in volta meccanismi il più possibile
semplici e funzionali che svolgono la stessa funzione, sia pur in modo approssimato, ha
costituito uno dei fondamenti del progresso tecnologico.
|
|
|