A.B. Kempe, How to draw a straight line,
London, 1877
 |
 |
|
La cella di Peaucellier si può ottenere dai due quadrilateri articolati in figura, ai quali la
tradizione ha dato i nomi di aquilone e dardo: sovrapponendoli ed identificando le due
aste più lunghe e quelle più corte otteniamo il meccanismo di Peaucellier.
|
|
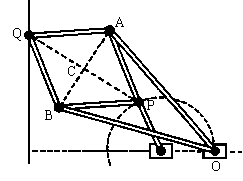
Le quattro aste della stessa lunghezza formano un rombo, le
due più lunghe sono incernierate a due vertici opposti del rombo e fra loro in un punto
fisso O, la settima asta costringe il punto P a muoversi su una circonferenza passante per
O. Al variare di P su tale circonferenza il punto Q si muove lungo una retta. E’
ovvio che i suoi punti O, P, Q sono sempre allineati al variare di P sulla circonferenza
passante per O. Si può dimostrare che vale la relazione OP . OQ = OA2 –
AP2 = costante. A tal proposito indichiamo con C il punto d’incontro delle
diagonali PQ ed AB del rombo APBQ. Le due diagonali si dividono scambievolmente per metà;
inoltre l’angolo ACP è retto. Poiché O, P, Q sono allineati si ha:
OP = OC – PC OQ = OC + CQ = OC + PC
Così:
OP . OQ = OC2
– PC2
ma per il teorema di Pitagora si ha:
OC2 = OA2 – AC2 PC2
= AP2 - AC2
Quindi:
OP . OQ = OA2 – AP2 = costante = K
Fatte queste premesse si può dimostrare che al variare di P sulla
circonferenza passante per O il punto Q descrive una retta.
|

|
Sia C il punto della circonferenza diametralmente opposto
ad O e sia P un generico punto della circonferenza diverso da C e da O. Indichiamo con Q e
D le posizioni assunte da un vertice del rombo (del meccanismo) quando il vertice opposto
coincide rispettivamente con P e C. Per quanto osservato precedentemente valgono le
seguenti relazioni:
OC . OD = K .
OP . OQ = K
Consideriamo i triangoli OPC e ODQ: essi sono simili e
quindi siccome l’angolo OPC è retto lo sarà anche l’angolo ODQ. Poiché il
punto P è stato arbitrariamente scelto sulla circonferenza passante per O, quanto detto
varrà per ogni punto del cerchio. Così al variare di P sulla circonferenza il punto Q si
sposta lungo una retta.
|



