La cicloide

Su un cerchio appoggiato a una retta orizzontale segniamo il punto più basso. Se ora muoviamo il cerchio lungo la retta, in modo che rotoli senza strisciare, il punto segnato si solleverà da terra fino ad arrivare a un'altezza massima uguale al diametro del cerchio, per poi riabbassarsi fino a toccare di nuovo il suolo a una distanza dal punto di partenza uguale alla circonferenza del cerchio. La curva descritta dal punto, che si ripete sempre uguale se si continua a far rotolare il cerchio, prende il nome di cicloide.

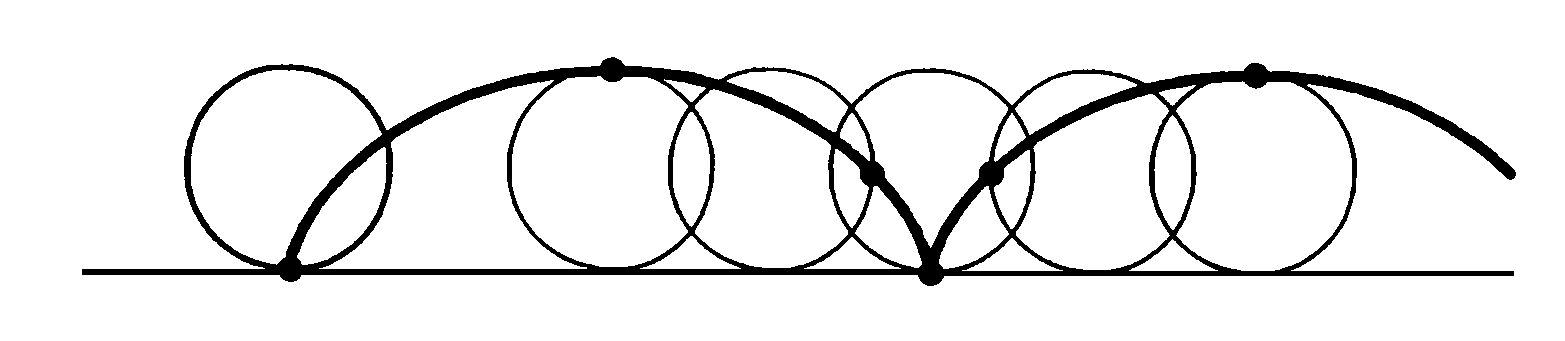Uno dei primi a prendere in considerazione questa curva fu Galileo, che nel 1640 scriveva: "Quella linea arcuata sono più di cinquant'anni che mi venne in mente il descriverla, e l’ammirai per una curvità graziosissima per adattarla agli archi d’un ponte. Feci sopra di essa, e sopra lo spazio da lei e dalla sua corda compreso, diversi tentativi per dimostrare qualche passione, e parvemi in principio che tale spazio potesse essere triplo del cerchio che lo descrive; ma non fu così, benché la differenza non sia molta".

In effetti, l’area dello spazio delimitato dalla cicloide, contrariamente a quanto pensava Galileo, che probabilmente aveva fatto degli esperimenti pesando dei modelli, è proprio il triplo di quella del cerchio generatore, come dovevano dimostrare quasi contemporaneamente E. Torricelli, G. Roberval e B. Pascal. Ben presto, oltre all'area, vennero trovati il centro di gravità. e i volumi dei solidi ottenuti facendola ruotare attorno alla base e all'asse, come anche un metodo per determinare le tangenti, una ricerca che vide impegnati i maggiori matematici del tempo, tra i quali R. Descartes (Cartesio).

Tutte queste ricerche testimoniano dell'interesse per una curva, forse la prima, totalmente moderna, che non si trova cioè nelle opere dei geometri classici Un interesse destinato ad aumentare notevolmente con la scoperta che essa costituiva la soluzione di due problemi a prima vista senza relazioni tra loro: l'isocronismo delle oscillazioni e la curva di discesa più rapida.

Il primo era un problema in gran parte tecnologico. La misura del tempo era infatti di grande importanza agli inizi dell'epoca moderna, dato che da essa dipendeva, in particolare, la determinazione della longitudine, essenziale per la navigazione oceanica. Verso la metà del Seicento, l’idea di costruire un orologio sfruttando le oscillazioni di un pendolo cominciava a diventare tecnicamente realizzabile.

Ora nel pendolo usuale, in cui il peso descrive un arco di cerchio, il periodo, cioè il tempo impiegato per compiere un'oscillazione completa, dipende dalla ampiezza di questa, ed è, maggiore per le grandi oscillazioni, va diminuendo via via che l'ampiezza diminuisce, e resta quasi costante per piccole oscillazioni. In altre parole, il pendolo circolare è isocrono solo approssimativamente, tanto più quanto più le oscillazioni sono piccole.

Ci si può allora chiedere: esiste una curva sulla quale tutte le oscillazioni, grandi e piccole, si svolgano nello stesso tempo? La risposta è affermativa: lo scienziato olandese Christian Huygens dimostrò che la curva isocrona è la cicloide, e di conseguenza che per ottenere delle oscillazioni strettamente isocrone occorre far muovere il pendolo lungo questa curva.

Ma come far muovere un pendolo lungo una cicloide? Si potrebbe costruire un profilo a forma di cicloide, lungo cui far rotolare il peso del pendolo, ma anche a non voler considerare la difficoltà di garantire un movimento regolare, l’attrito del peso lungo il profilo basterebbe a fermare il movimento dopo pochissime oscillazioni. Se invece attacchiamo il peso a un estremo di una cordicella, che appendiamo per l’altro estremo, il pendolo descriverà un cerchio, che non e' isocrono.

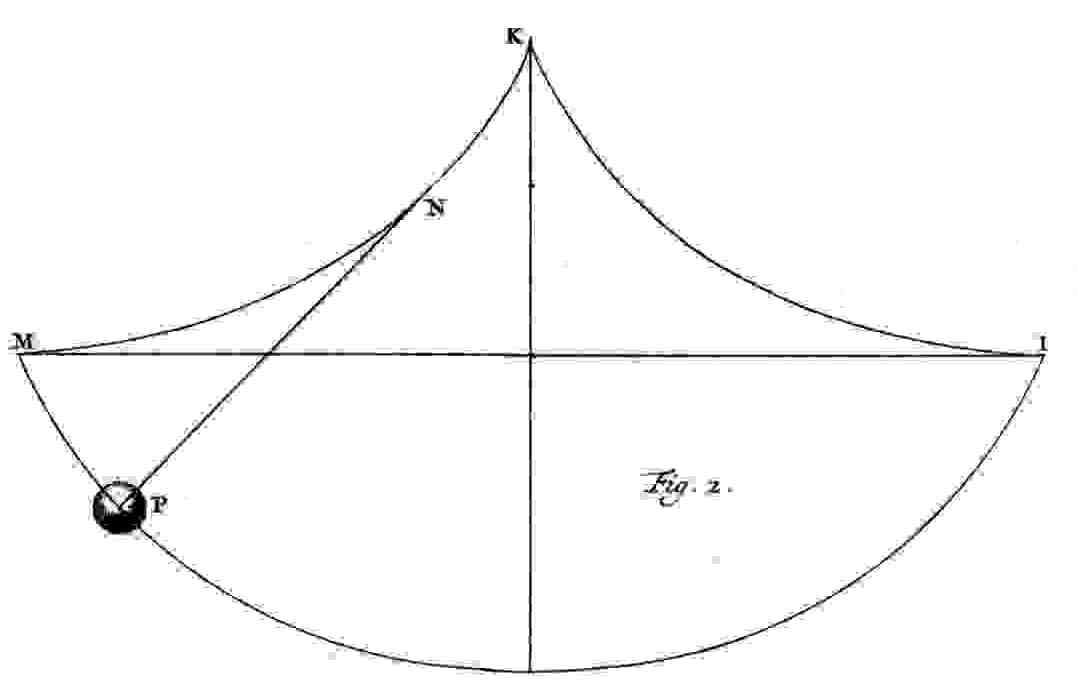
Il problema si risolve costruendo due guide, che si mettono dalle due parti del punto di sospensione; in questo modo il filo del pendolo non sarà libero di muoversi, ma dovrà seguire in parte la guida: si tratta allora di costruire un profilo tale che l’estremità del pendolo descriva una cicloide. Dal punto di vista della geometria, occorrerà costruire una curva (il profilo) tale che la sua evolvente sia una cicloide. Huygens dimostra che ciò avviene se il profilo è ancora una cicloide: costruendo quindi due guide a forma di cicloide si otterrà, un pendolo perfettamente isocrono.

L'altro problema di cui la cicloide fornisce la soluzione è la determinazione della cosiddetta brachistocrona, ovvero la curva che rende minimo il tempo di caduta da uno dei due estremi all'altro.

Più precisamente, supponiamo di fissare due punti A e B, il primo posto più in alto del secondo, ma non sulla verticale, e lasciamo cadere da A un grave che giunga a B scivolando su una curva che unisce i due punti. Poniamoci ora il seguente problema: tra tutte le curve che uniscono A e B, qual è quella che rende minimo il tempo di caduta? Non è, come potrebbe sembrare a prima vista, la retta che unisce i due punti; infatti, per diminuire il tempo di caduta conviene iniziare quasi verticalmente, in modo da acquistare subito velocità, anche a scapito della maggior lunghezza del cammino.

La soluzione di questo problema costituì uno dei primi successi del calcolo differenziale, che verso la fine del Seicento era stato inventato indipendentemente da I. Newton e da G.W. Leibniz. Il problema venne enunciato per la prima volta da Johann Bernoulli, sotto forma di sfida ai matematici del tempo.

La sfida di Bernoulli venne raccolta dai maggiori matematici del tempo, tra i quali gli stessi Leibniz e Newton, che ne dettero una soluzione per mezzo del calcolo infinitesimale, dimostrando che il profilo, lungo il quale il tempo di caduta è minimo, è una cicloide.

Quest'ultima è una curva trascendente, della quale Leibniz e Bernoulli trovano 1'equazione differenziale; se indichiamo con x ed y le coordinate di un punto generico sulla cicloide, e con x+dx e y+dy quelle di un secondo punto infinitamente vicino al primo, si ha:

Si può trovare un'equazione parametrica della cicloide nel modo che segue. Consideriamo il cerchio generatore, che per comodità supporremo di raggio 1, ad un punto del suo percorso. Se indichiamo con P il punto sulla curva, di coordinate (x, y), e con t la misura (in radianti) dell'angolo PÔB, uguale alla lunghezza dell’arco PB, risulta AB = PB, BC = PQ e PC = BQ. Si ha allora:

x = AC = AB - BC = t - PQ = t -.sen t

y = PC = QB = OB - OQ = 1 – cos t

Quando il cerchio fa un giro intero, la lunghezza t varia tra 0 e 2p ; il punto di coordinate (t-sen t, 1-cos t) descrive la cicloide.
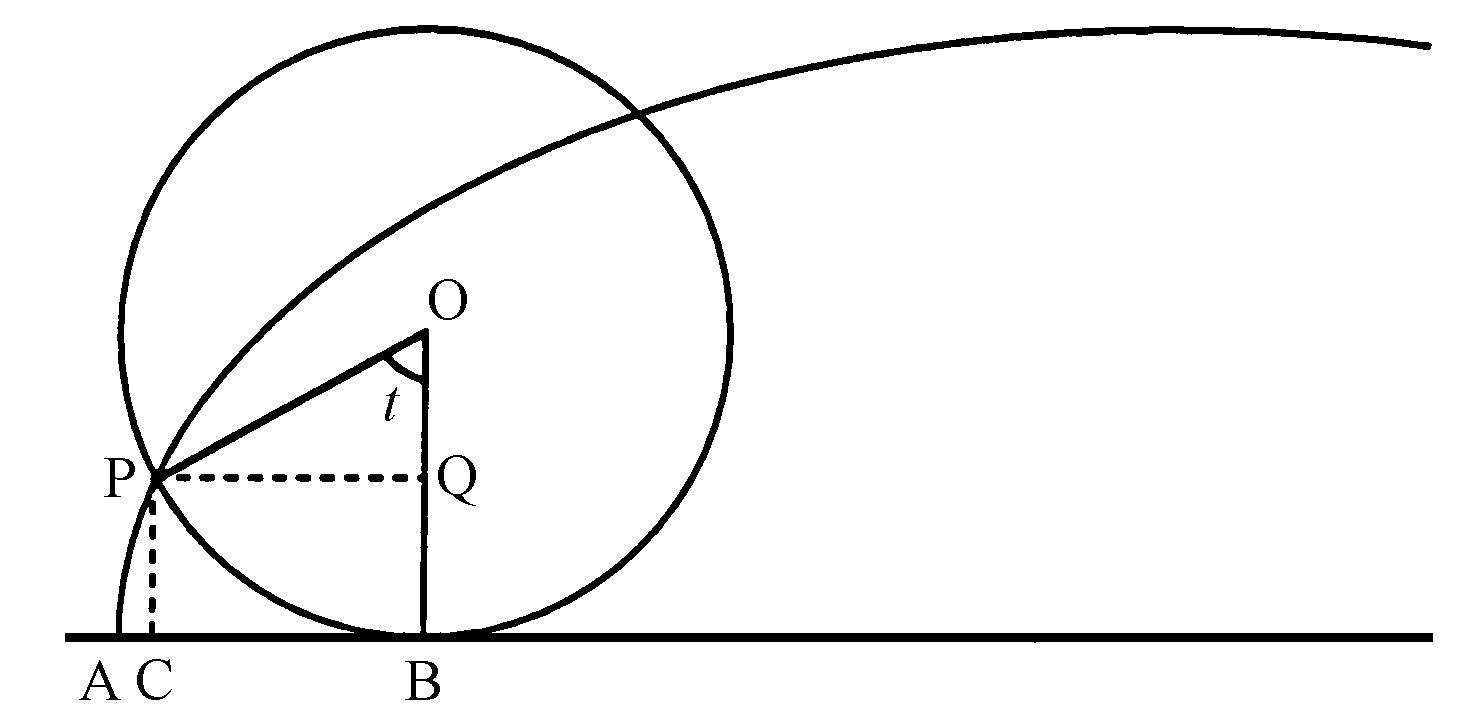