Il funzionamento del "Risolutore universale di equazioni"
Dal punto di vista matematico, il funzionamento della macchina è semplice e sfrutta ingegnosamente la similitudine di opportuni triangoli rettangoli. Per semplicità, esponiamo il ragionamento nel caso di un polinomio di 2° grado. Supponiamo dunque di voler tracciare il grafico del polinomio p(x) = ax2+bx+c per valori di x compresi, ad esempio, tra 0 ed 1; i coefficienti a, b, c saranno presi, per maggior chiarezza, tutti positivi. Riferendoci alla figura 1, fissato un qualsiasi numero x tra 0 ed 1, denotiamo con X, I i punti sull’asse x di ascisse x, 1, e tracciamo per tali punti le perpendicolari r, s all'asse x. Indichiamo poi con A, B, C i punti sull'asse y di ordinate a+b+c, b+c, c rispettivamente, e tracciamo nell'ordine: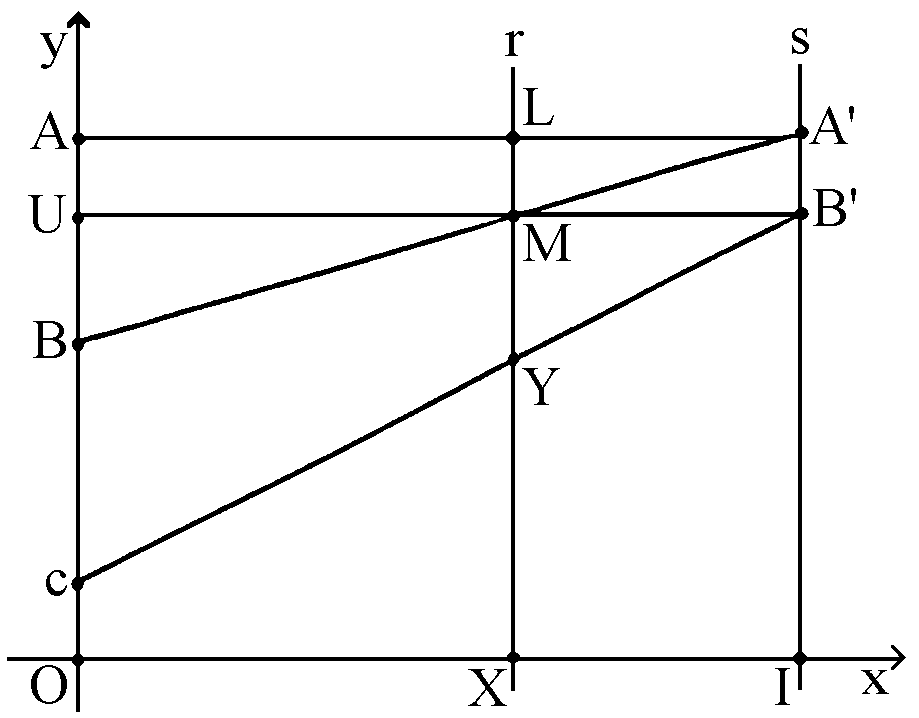 |
- il segmento AA', parallelo all'asse x, che interseca r in L;
- il segmento BA', che interseca r in M;
- il segmento UB', parallelo per M all’asse x;
- il segmento CB', che interseca r in Y.
Y ha coordinate (x, ax2+bx+c), cioè giace sul grafico del polinomio p(x). Variando la scelta di x (il che nella macchina si ottiene muovendo il telaio longitudinalmente), il luogo dei punti Y così costruiti fornirà allora il grafico cercato.
Infatti, osservando che
![]()
avremo: per la similitudine dei triangoli MLA' e BAA'
![]()
mentre per la similitudine dei triangoli YMB ' e CUB'

Pertanto:

 |