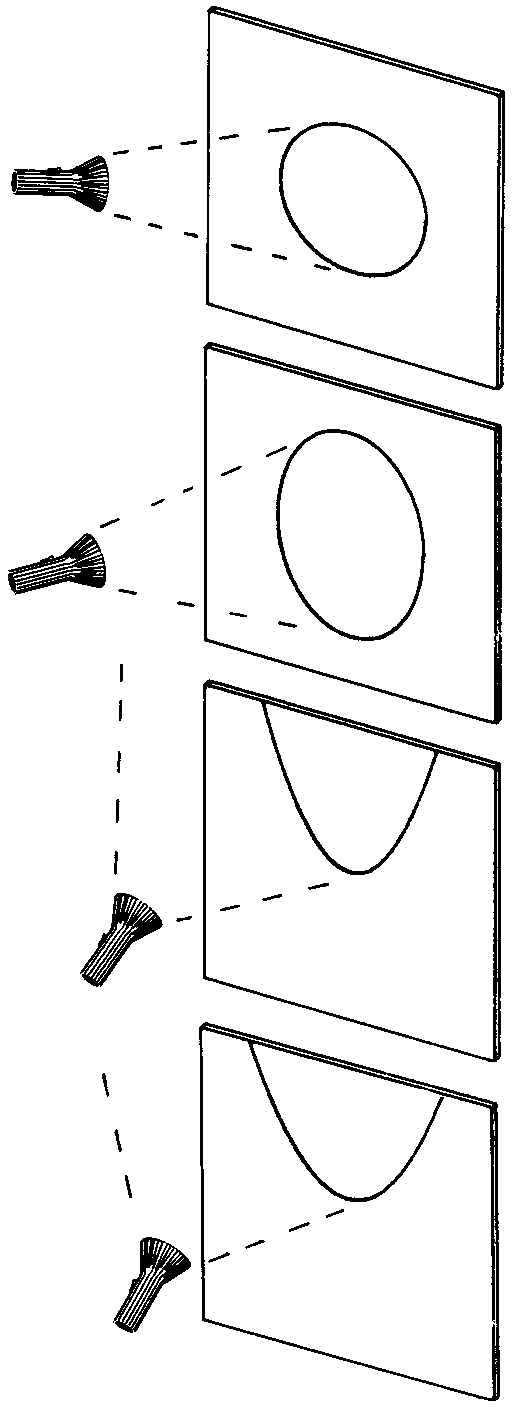
Se accendiamo una torcia elettrica, la luce della lampadina, uscendo dalla lente di forma circolare, formerà un cono di luce che ha come vertice il filamento della lampadina, e come asse la retta che passa per quest’ultimo e per il centro della lente. Supponiamo ora di dirigere il raggio luminoso verso una parete; la parte illuminata assumerà forme diverse, a seconda dell’inclinazione dell’asse, e precisamente: se il muro viene illuminato perpendicolarmente (ovvero se l’asse del cono di luce è perpendicolare alla parete), la figura che si forma è un cerchio, tanto più grande quanto maggiore è la distanza della lampadina dalla parete. se ora cominciamo ad inclinare la torcia, il cerchio si deforma assumendo una forma delimitata da una linea dapprima quasi circolare, poi sempre più allungata: si tratta di un’ellisse che diventa sempre più allungata (eccentrica), fin quando il raggio più esterno del fascio di luce diventa parallelo alla parete. Abbiamo in questo momento una parabola. Basta girare ancora un po’, e il raggio più esterno ora diverge dalla parete, e abbiamo un’iperbole, o meglio uno dei due rami dell'iperbole.   Queste quattro curve prendono il nome di sezioni coniche, dato che esse appaiono come sezioni di un cono (il cono di luce) con un piano (della parete). Questi oggetti, di proprietà del Dipartimento di Matematica di Firenze, sono stati realizzati a Dresda negli anni Cinquanta.