Spirali

Se c'è una curva che si avvicina a toccare i punti più nascosti della psiche umana, questa è senza dubbio la spirale. Curva ambigua e duplice, da una parte essa dà l’immagine dell'espansione e della totalità; una curva che ruotando si conserva sempre simile a sé stessa, ma che allo stesso tempo va allargandosi e distendendosi all'infinito, quasi che nel ruotare sempre nuove parti nascessero dal centro per muoversi in giro verso la periferia. Così la spirale è simbolo del sole, i cui raggi penetrano e vivificano l’universo.Ma accanto a questa faccia limpida e serena, la spirale ne mostra una seconda oscura .e inquietante: il movimento si trasforma da un'espansione a una contrazione continua che ipnoticamente fa precipitare nel centro, e induce metafore inquietanti e drammatiche: la spirale del vizio, della follia.

A dispetto di queste sue immagini contrapposte, la generazione delle linee spirali è delle più semplici, un raro esempio di profondità psicologica e contemporaneamente di evidenza geometrica; due motivi che hanno spinto i matematici a studiarne le proprietà fin dall'antichità, indipendentemente dalle sue scarse applicazioni. La prima e più semplice delle linee spirali è quella studiata da Archimede, e che porta il suo nome: la spirale archimedea.

Spirale di Archimede

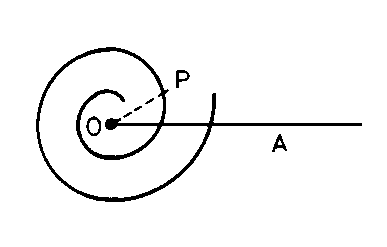Essa si genera quando un mobile P si muove a velocità uniforme v su un'asta, che a sua volta ruota uniformemente attorno a un suo punto, con velocità angolare w . Se indichiamo con r_o la posizione iniziale del punto sull'asta (misurata a partire dal centro di rotazione), e con q l’angolo iniziale, avremo

r = r_o + v t

q = q_o + w t

da cui, ricavando t dalla seconda equazione e sostituendo nella prima, si ottiene l’equazione della curva descritta dal mobile:

r = r_o + v/w (q - q_o)

In particolare, se si misurano gli angoli a partire dalla posizione iniziale (q _o = 0) e il mobile parte dal centro (r_o = 0), si ha 1'equazione (in coordinate polari):

r = (v/w) q

nella quale r rappresenta la distanza dal centro di rotazione, e q l’angolo contato a partire dalla posizione iniziale.

Altre spirali si ottengono supponendo che il moto lungo l’asta sia accelerato in vari modi, ad esempio che si abbia r = a t² (spirale quadratica), o più in generale r = a tⁿ.

In questo caso, sempre supponendo q _o = 0, si ottiene 1'equazione:

r = (a/wⁿ) qⁿ

Tutte queste spirali partono dal centro di rotazione e vanno allontanandosi sempre più via via che l’angolo q cresce. Di genere diverso è la spirale logaritmica, la cui equazione è:

q = log_A t

ovvero

r = A^q (con A > 1).

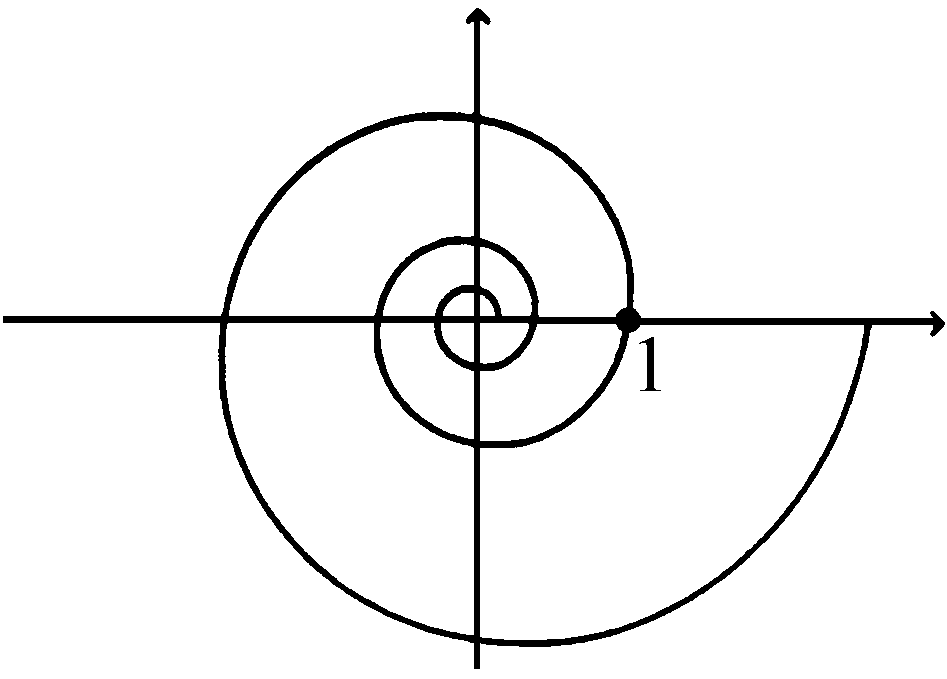
Questa spirale non parte dal centro come le altre, ma si trova inizialmente (cioè, per q = 0) a distanza 1 da questo. Via via che q cresce, la spirale logaritmica si allontana dal centro come le precedenti, anche se molto più velocemente; quando poi q diventa negativo aumentando in valore assoluto, il punto descrive infinite rivoluzioni avvicinandosi sempre più al centro, senza mai giungervi: la spirale logaritmica è infinita nei due versi.

Spirale logaritmica