| |
|
|


|
Un problema di cui la cicloide fornisce la soluzione è
la determinazione della cosiddetta brachistocrona, ovvero la curva che rende minimo
il tempo di caduta da uno dei due estremi all'altro. Più precisamente, supponiamo di
fissare due punti A e B, il primo posto più in alto del secondo, ma non sulla verticale,
e lasciamo cadere da A un grave che giunga a B scivolando su una curva che unisce i due
punti. Poniamoci ora il seguente problema: tra tutte le curve che uniscono A e B, qual è
quella che rende minimo il tempo di caduta? Non è, come potrebbe sembrare a prima vista,
la retta che unisce i due punti; infatti, per diminuire il tempo di caduta conviene
iniziare quasi verticalmente, in modo da acquistare subito velocità, anche a scapito
della maggior lunghezza del cammino.
L'exhibit mostra che tra due biglie di
acciaio lasciate cadere contemporaneamente dal punto A, una lungo una pista rettilinea e
l'altra lungo una cicloidale, quest'ultima è quella che raggiunge per prima il punto B.
|
|
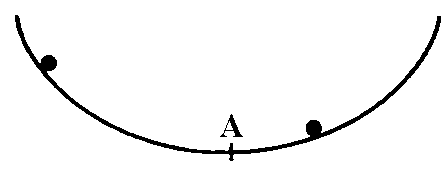
L'exhibit mostra anche un'altra notevole
proprietà della cicloide (tautocrona): per questa curva il tempo impiegato da un
grave per raggiungere il suo punto più basso è indipendente dal punto di partenza.
Qualunque sia la loro posizione di partenza, le due sferette si incontrano nel punto A.
|
|
|