All'inizio del conto / Quando l'uomo imparò a contare

Laboratori sui sistemi di numerazione e di conto rivolti alle classi elementari del primo e secondo ciclo, alle medie inferiori, al biennio delle superiori e alla scuola dell'infanzia

Numeri e conti presso gli antichi sumeri

Uno dei più rudimentali strumenti di conto è costituito da piccole pietre o sassolini.
In Mesopotamia questo sistema viene raffinato: si costruiscono con l'argilla calculi di forme differenziate con valori assegnati.
Da questa forma di rappresentazione "concreta" dei valori si passa gradualmente a una vera e propria forma di scrittura simbolica, mentre i calculi continuano ad essere impiegati come ausilio nei conti.

Nei laboratori:si ripropone il sistema dei sumeri per la rappresentazione dei numeri e il passaggio dai “calculi” alla scrittura su tavoletta; si utilizzano i “calculi” come strumento per eseguire alcuni conti, da semplici addizioni a complesse divisioni.

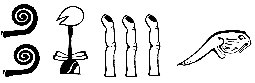
I geroglifici degli antichi egizi

Per scrivere i numeri gli antichi egizi si servivano di simboli speciali che appaiono su monumenti e iscrizioni fin dall'inizio del III millennio. La numerazione era fondata su una base rigorosamente decimale e prevedeva la combinazione di simboli corrispondenti ai valori 1, 10, 100, 1000, 10000, 100000, 1000000.

Nei laboratori: si presenta il sistema di rappresentazione degli egizi; si sperimentano le tecniche di conto, in particolare quella per la moltiplicazione che era eseguita tramite successivi raddoppi.

Numeri e abachi degli antichi romani

Per scrivere i numeri gli antichi romani utilizzavano la scrittura che è rimasta fino ad oggi in uso, specialmente nell'indicazione dei numeri ordinali, che combina i simboli I, V, X, L, C, D, M e altri ancora per i valori più alti. Per eseguire i calcoli usavano strumenti, noti come abachi, in cui le quantità venivano registrate per mezzo di palline o chiodini posizionati opportumente in colonne.

Nei laboratori: si presenta il sistema di scrittura dei romani; si utilizzano riproduzioni di antichi abachi romani per la rappresentazione delle quantità si sperimentano le tecniche di conto sull'abaco e per scritto.

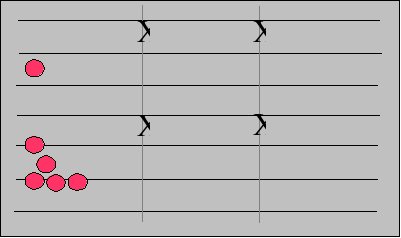
Le tavole di conto

Le tavole di conto sono dei semplici ed efficaci ausili per il calcolo che, sotto forme diverse, si ritrovano dall'antichità fino al Rinascimento e trovano impiego soprattutto nella contabilità. Sono essenzialmente costituite da un piano d'appoggio suddiviso in righe o colonne sulle quali si collocano dei gettoni; a seconda della riga (o colonna) in cui si trova, il gettone assume un valore diverso.

Nei laboratori: si utilizzano tavole di conto per registrare dei numeri; si scopre come attraverso delle semplici regole di posizionamento dei gettoni si può facilmente ottenere il risultato di operazioni senza eseguire nessun calcolo.

Pallottolieri giapponesi

Parente prossimo del nostro pallottoliere e probabilmente discendente da un unico antenato già diffuso nel mondo antico, il soroban – così come la versione cinese di nome suan pan – è un efficacissimo strumento di calcolo che in mani abili ed esperte gareggia in rapidità con le moderne calcolatrici.

Nei laboratori: si prende confidenza con il soroban; si provano alcune semplici operazioni, dalle addizioni alle moltiplicazioni a più cifre.

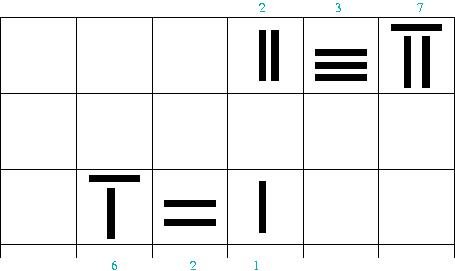
Bastoncini cinesi per numeri e conti

Si tratta di uno strumento per il calcolo diffuso in Cina dall'antichità fino ad un'epoca relativamente recente. È costituito da una tavoletta quadrettata su cui, per rappresentare i numeri, si dispongono opportunamente dei bastoncini (originariamente in avorio o bambù)

Nei laboratori: i più piccoli possono rapidamente imparare a contare con i bastoncini; si può arrivare poi ad eseguire qualche operazione anche piuttosto complessa.

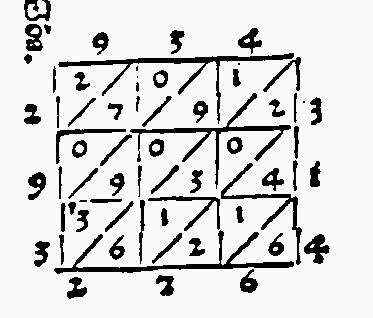
Tecniche varie di moltiplicazione

Gli algoritmi per le operazioni che apprendiamo a scuola non sono gli unici possibili; molti altri sono stati eleborati ed utilizzati nel corso di secoli di storia. In particolare la moltiplicazione presenta un grandissimo numero di procedimenti alternativi, alcuni dei quali per certi aspetti più semplici ed anche più divertenti del nostro. Nei laboratori: moltiplicazioni a non finire con tecniche varie, da quelle dei matematici indiani alle varianti arabe, da quelle dei maestri d'abaco a quelle dei contadini russi ...

Bastoncini per moltiplicare e dividere

All'inizio del Seicento John Napier inventò i celebri bastoncini che opportunamente combinati facilitano l'esecuzione di una moltiplicazione rendendo superflua la conoscenza delle tabelline, un preludio alla nascita, pochi decenni più tardi, delle prime macchine calcolatrici meccaniche.

Nei laboratori: le moltiplicazioni si fanno da sole con i bastoncini di Nepero e ancor più con quelli di Genaille-Lucas, una variante di inizio Ottocento; lo stesso vale per le temute divisioni.