Un museo per la matematica
| Il giardino di Archimede
Un museo per la matematica |
La parte infinitesima di cui è continuamente aumentata o diminuita una quantità variabile è chiamata differenza di quella quantità [...]Vengono poi esposte le regole di differenziazione per le ordinarie operazioni e le successive sezioni del volume sono dedicate alla applicazione del calcolo a problemi geometrici come la ricerca delle tangenti, la determinazione di massimi, minimi e flessi di una curva, lo studio della curvatura, delle evolute, delle caustiche, degli inviluppi.
È evidente che la differenza di una quantità costante è nulla o zero, ovvero (ciò che è la stessa cosa) le quantità costanti non hanno differenza[...].
I. Richiesta o supposizione
Si richiede che due quantità la cui differenza è infinitesima possano essere usate indifferentemente l'una per l'altra [...]
II. Richiesta o supposizione
Si richiede che una linea curva possa essere considerata come la collezione di una infinità di linee rette, ciascuna infinitesima, ovvero (ciò che è la stessa cosa) come poligono di un numero infinito di lati, ciascuno infinitesimo, che tramite gli angoli tra essi formati determinano la curvatura della linea [...]
 Guillaume Francois de L'Hospital
Guillaume Francois de L'Hospital
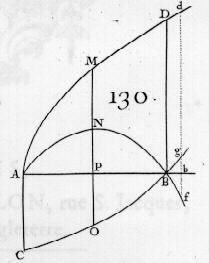
Sia AMD (AP=x, PM=y, AB=a) una linea curva tale che il valore dell'applicata y sia espresso da una frazione il cui numeratore e denominatore diventano ciascuno zero quando x=a, ossia quando il punto P cade sul punto dato B. Si domanda quale debba essere allora il valore dell'applicata BD.


|
Johann Bernoulli
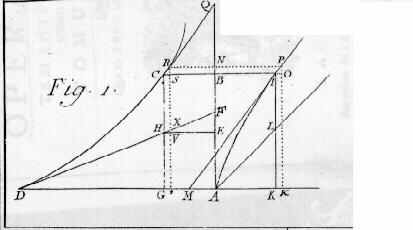
Solutio problematis Cartesio Propositi in Opera [...] Il problema è dunque il seguente: trovare la curva AI tale che la sua ordinata KI sta alla sottotangente KM come un segmento dato N sta al segmento IL dell'ordinata individuato dalla curva AI e dalla retta AL che forma con l'asse AK un angolo pari alla metà di un angolo retto. |
I geometri hanno fino ad ora utilizzato il metodo dei massimi e minimi per quei problemi in cui fra infinite parti o funzioni di una sola curva data se ne cerca una massima o minima; ma non hanno pensato di applicarla laddove fra le infinite curve non date se ne cerca una a cui competa un qualche massimo o minimo.
|
|
Jacob Bernoulli
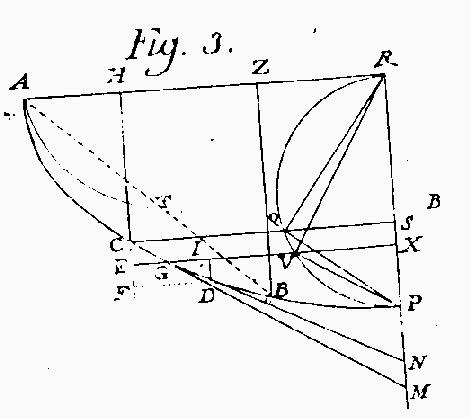
De curva celerrimi descensus Nello svolgimento proponiamo al celebre Nieuwentijt l'uso dei differenzio-differenziali (che egli ingiustamente rifiuta), laddove siamo costretti ad assumere che il pezzetto GL sia ancora più piccolo di EG e GI già essi stessi infinitamente piccoli; senza di ciò, non vedo come si possa svelare la soluzione del problema. Sono infatti EG, GI elementi dell'ascissa AH, così come CG, GD sono elementi della curva stessa, e HC, HE elementi della stessa sua applicata, e CE, EF sono i loro elementi; così che ricondotto il problema alla geometria pura ci si riduce a trovare la curva i cui elementi siano direttamente proporzionali agli elementi delle ascisse e inversamente proporzionali agli elementi delle ordinate; in verità osservo che gode di questa proprietà l'isocrona di Huygens, da ora in poi anche oligocrona, e comunemente nota ai geometri come cicloide [...] |
Chiamo funzione di una grandezza variabile una quantità composta in una maniera qualunque da questa grandezza variabile e da costanti.È però con Eulero che il concetto di funzione prende il sopravvento su quello meno duttile di relazione. La definizione data all'inzio dell' Introductio in analysin infinitorum è quella di un'espressione analitica costruita a partire dalla variabile
Affinché questa spiegazione possa essere anche più ampia, oltre alle potenze di z che hanno esponenti positivi, ogni potenza qualunque dovrebbe essere ammessa. Allora non ci sarà più alcun dubbio che ogni funzione di z possa essere trasformata in un'espressione infinita di questo tipo:
doveL'idea di funzione è ancora lontana da quella moderna: un'importanza preponderante è assunta dal fatto che una funzione sia descrivibile nel suo intervallo di definizione per mezzo di un'espressione analitica singola. Solo più tardi, a seguito di varie discussioni riguardanti in particolare la corda vibrante, Eulero accetterà la possibilità di funzioni cosiddette ``discontinue'', cioè descritte da un'espressione in un intervallo e da una diversa in un altro.,
,
,
... denotano numeri qualunque.

|
Leonard Euler
Introductio in analysin infinitorum Una quantità costante è una quantità determinata che conserva sempre lo stesso valore. |