Un museo per la matematica
| Il giardino di Archimede
Un museo per la matematica |
Ma ho anche inserito di quando in quando anche i dx, dy caratteristici del calcolo differenziale e il loro modo di essere differenziati e sommati. E così, se anche li avessi potuti introdurre anche nei miei opuscoli precedenti! Ma allora i segreti di quel metodo mi erano inaccessibili, mentre ora, provata la loro utilità e fecondità, perché non inserirli tra gli altri metodi a me familiari? Inoltre il significato dei simboli è molto chiaro, poiché non significa altro se non una differenza infinitamente piccola tra le stesse x e y, e facilmente troverai esposte le regole stesse del calcolo se osserverai e sfoglierai attentamente questo trattato, nel caso in cui tu non volessi ricorrere al chiarissimo L'Hospital che le spiega in modo più completo nel trattato degli infinitamente piccoli.L'utilizzo dei metodi differenziali resta in effetti piuttosto sporadico. Un'occasione per esporne alcuni rudimenti è costituita da una lettera ricevuta da Gabriele Manfredi sulla quadratura dell'iperbole che viene inserita nella seconda parte dell'opera. Per chiarire il procedimento esposto da Manfredi, Grandi infatti aggiunge una serie di note in cui spiega i passaggi e descrive le regole del nuovo calcolo.
 Guido Grandi
Guido Grandi
(*) Infatti la ``differenza'' di una qualunque potenza dell'incognita x è la stessa potenza moltiplicata per il suo esponente e ``differenziata'' di una sua dimensione, lasciando invariate le costanti per cui è moltiplicata, costanti in verità per le quali la ``differenza'' è nulla, come è dimostrato nel Tractatu de infinitis infinitorum et infinite parvorum nello scolio alla prop. V, e dunque differenziando questa serie [ecc. ] si ottiene quella precedente
ecc.
 Iacopo Riccati
Iacopo Riccati
Caso I
Sia generalmente proposta l'equazione di tre membri.
Seallora siamo nel caso sciolto dal Signore Manfredi; ma sopposto che non ci sia fra le somme degli esponenti la necessaria egualità, cerchiamo almeno in quali casi con un poco di artifizio ci può venir fatto di trasformare la formola proposta in una equivalente, in cui si verifichi la condizione prescritta. Così se non potremo separare generalmente le variabili, determineremo però infiniti casi, ne' quali la separazione succede felicemente.
 Giulio Carlo de' Toschi Fagnano
Giulio Carlo de' Toschi Fagnano
Supposizioni note agli intendenti del calcolo infinitesimale. - Sia la lemniscata(figura 24), il cui semiasse
; si sa che prendendo nel centro C l'origine dell'abscisse
e chiamando
le ordinate che sono all'asse normali, la natura della lemniscata s'esprima con quest'equazione
. Si sa ancora che se si chiama
la corda indeterminata
si ha l'arco diretto
e l'arco inverso
. [...]
Non avvi alcuno il quale informato essendo delle Matematiche cose non sappia altresì quanto, in oggi spezialmente, sia necessario lo studio dell'analisi e quali progressi si sieno con questa fatti, si facciano tuttora, e possano sperarsi nell'avvenire; che però non voglio né debbo trattenermi qui in lodando questa scienza, che punto non ne abbisogna, e molto meno da me. Ma quanto è chiara la necessità di lei, onde la Gioventù ardentemente s'invogli di farne acquisto, grandi altrettanto sono le difficoltà che vi s'incontrano, sendo noto e fuor di dubbio che non ogni città, almeno nella nostra Italia, ha persone che sappiano o vogliano insegnarla e non tutti hanno il modo di andar fuori della Patria a cercarne i maestri.Con l'intenzione dunque di raccogliere e riordinare con chiarezza e semplicità, omettendo tutto il superfluo, senza lasciare cosa alcuna che esser possa utile o necessaria sono redatti i due tomi. Il primo s'intitola Dell'analisi delle quantità finite, e contiene elementi di algebra e geometria analitica con lo studio di varie curve tra cui la versiera a cui è rimasto legato il nome dell'Agnesi. Il secondo riguarda invece il calcolo ed è diviso nei tre libri Del calcolo differenziale,Del calcolo integrale, Del metodo inversof delle tangenti.

|
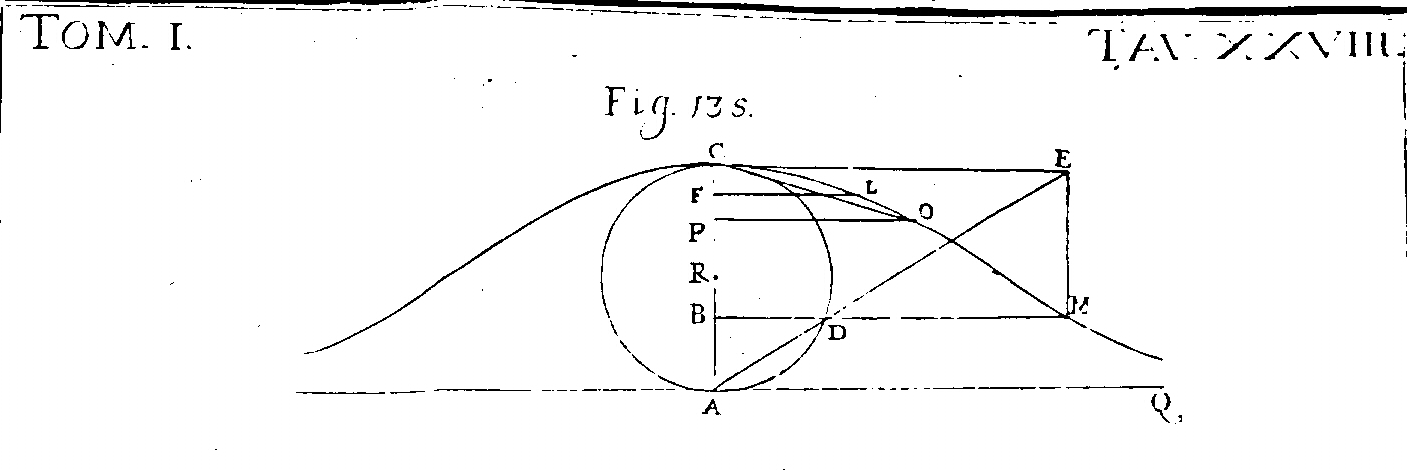
Maria Gaetana Agnesi
Istituzioni analitiche ad uso della gioventù italiana Dato il semicircolo ADC del diametro AC si ricerca fuori di esso il punto M tale che condotta MB normale al diametro AC che taglierà il circolo in D, sia AB:BD=AC:AM, e perché infiniti sono i punti M che soddisfanno al problema, se ne dimanda il luogo. [...]L'Agnesi determina l'equazione |