Il giardino di Archimede
 Un museo per la matematica

I fondamenti del calcolo

Nel 1734 il filosofo e vescovo irlandese George Berkeley pubblica un opuscolo intitolato The Analist , scritto sotto forma di ``discorso rivolto a un matematico infedele'' (probabilmente l'astronomo Halley) in cui la fondatezza del calcolo viene fatta oggetto di dura e puntuale critica. Berkeley centra con molta precisione il principale punto debole della costruzione newtoniana, così come di quella dei ``matematici stranieri'', cioè dei collaboratori di Leibniz. Si tratta rispettivamente della definizione stessa di flussione e di incrementi infinitesimi.
Per calcolare la flussione di una funzione $f(x)$ si deve infatti calcolare il rapporto incrementale $\frac{f(x+e\dot{x})-f(x)}{e}$ e poi porre $e=0$. Ma dividendo per $e$ si fa tacitamente l'ipotesi che $e$ non sia nullo e una volta effettuata la divisione non è lecito dunque, osserva Berkeley, porre $e=0$. La mancanza di una precisa teoria dei limiti rende difficile il superamento del paradosso.
L'altra definizione newtoniana, basata sulle prime e ultime ragioni, prevede invece la considerazione del rapporto non quando e è uguale a zero, né quando e è diverso da zero, ma nel momento stesso in cui si annulla e il triangolo caratteristico si contrae in punto. Di questa formulazione ancora più oscura Berkeley si fa facilmente gioco:
Questo è assolutamente inconcepibile, afferma. Eppure vi sono alcuni i quali mentre esprimono disappunto all'enunciazione di qualsiasi mistero, per quanto li concerne non fanno alcuna difficoltà, capaci di scolare un moscerino e di inghiottire un cammello [...]
E più avanti:
E che cosa sono queste flussioni? Le velocità di incrementi evanescenti. E che cosa sono questi incrementi evanescenti? Essi non sono quantità finite, non sono infinitesimi, non sono niente. E allora non dobbiamo forse chiamarli gli spettri di quantità morte?
La critica di Berkeley non si limita all'attacco puro e semplice ai fondamenti del calcolo; essa deve infatti discutere le ragioni del successo della nuova analisi nell'affrontare e risolvere problemi con un'ampiezza prima neanche immaginabile. Egli tenta allora di spiegare come da principi così precari possano discendere risultati tanto sorprendenti. Per Berkeley questi successi sono dovuti a una compensazione degli errori. Supponiamo ad esempio di voler trovare la tangente a una curva $y(x)$, ossia la sua sottotangente, cioè il segmento AP. Dalla proporzionalità dei triangoli ABP e BRT si ha $AP=BP \cdot BR/TR=ydx/TR$. Ora, dice Berkeley, si commette un primo errore scrivendo $SR=dy=y(x+dx)-y(x)$ al posto di TR, un errore che non può essere trascurato se $dx$ è diverso da zero. D'altra parte, dopo aver fatto le dovute semplificazioni, nel quoziente$ dx/dy$ si pone $dx=0$: un secondo errore che compensa il primo e che conduce al risultato esatto $AP=y/y'$.
La mutua cancellazione dei due errori porta dunque a risultati esatti e si arriva ``se non alla scienza, almeno alla verità''; una tesi che verrà ripresa anche da Lazare Carnot nei Refléxions sur la métaphysique du calcul infinitesimal del 1797, dove alla elisione fortuita sostituirà una teoria della necessità della compensazione degli errori per dare al calcolo una base sicura.
Le tesi di Berkeley condizionano non poco il corso dell'analisi inglese; se matematici poco dotati prendono le difese della teoria con argomentazioni in genere ripetitive e superficiali, altri si impegnano a fondo in vani tentativi di eliminare le controverse flussioni dall'analisi. Fra questi, Colin MacLaurin che nel 1742 in difesa del metodo di Newton pubblica il Treatise of fluxions, dove tenta un'esposizione sistematica in termini rigorosamente geometrici della teoria delle flussioni evitando infiniti e infinitesimi, primi e ultimi rapporti e basandosi sulla velocità istantanea.
Ben diversa è la situazione sul continente dove premature discussioni sui principi attecchiscono solo marginalmente mentre con la nuova analisi vengono aggrediti tutti i campi della scienza e in primo luogo della fisica e si registra uno sviluppo contemporaneo e senza pari di metodi e tecniche del calcolo, che per un certo periodo si identifica con la matematica nella sua totalità.
Nella mole dei risultati ottenuti in circa mezzo secolo si cominciano però via via ad avvertire debolezze nella teoria in particolare per quel che riguarda i rapporti tra serie di funzioni e continuità, che divengono inaccettabili dopo il trattato di Fourier sulla propagazione del calore, tanto che l'Accademia di Berlino offre un premio per il miglior lavoro sui fondamenti del calcolo.
Nella discussione intervengono matematici come D'Alembert che esprime la sua posizione in vari articoli dell'Encyclopédie. Alla voce ``limite'' egli sostiene che ``la teoria dei limiti è la base della vera metafisica del calcolo differenziale''.
Una posizione diversa è presentata da Lagrange nella Note sur la métaphysique du calcul infinitésimal e poi sviluppata nella Théorie des fonctions analytiques (1797) che costituisce il più compiuto tentativo di sistemazione rigorosa dell'analisi prima dell'intervento definitivo di Cauchy. Qui egli premette una dettagliata critica alle concezioni dei fondatori del calcolo basate sugli infinitesimi e tenta invece di evitare le difficoltà usando gli sviluppi in serie. La ``derivata'' (il termine compare qui per la prima volta) viene introdotta sviluppando la funzione $f$ nel punto $x_o$, $f(x)=a_o +a_1 (x- x_o)+a_2 (x-x_o)^2+...$, i coefficienti $a_o$, $a_1$, $a_2$, ... dipenderanno da $x_o$; di questi $a_o$ è il valore della funzione nel punto $x_o$, mentre, per definizione, si dice derivata della $f$ in $x_o$ il coefficiente $a_1$, e si indica con il simbolo $f'(x_o)$.
L'impostazione di Lagrange viene contestata e rovesciata nella sistemazione dovuta indipendentemente a Augustin Louis Cauchy e a Bernhard Bolzano.
Nel 1817 Bolzano pubblica l'opuscolo, Rein analytischer Beweis des Lehrsatzes in cui, per dare una dimostrazione del teorema degli zeri, introduce in maniera rigorosa alcuni concetti come quello di continuità delle funzioni, di convergenza delle successioni e delle serie, di estremo superiore. I contributi di Bolzano rimasero però poco conosciuti e furono riscoperti solo più tardi.
Ben diversa è invece l'influenza dei lavori di Cauchy, che segnano un punto di svolta nel calcolo infinitesimale, determinando in gran parte il successivo corso della teoria. Nel 1821 viene pubblicato il primo dei tre trattati scritti da Cauchy per gli studenti dei suoi corsi, il Cours d'analyse de l'École Polytechnique. Secondo quella che era stata anche la visione di d'Alembert, il concetto di limite viene posto a base di tutte le costruzioni dell'analisi: per mezzo di esso Cauchy definisce la controversa nozione di infinitesimo e quella di infinito, definisce la continuità di funzione e studia la convergenza di serie e successioni. Nel successivo Résumé des leçons sur le calcul infinitesimal (1823) la teoria dei limiti è applicata al calcolo infinitesimale: la ``derivata'', pur conservando la terminologia lagrangiana, viene ora rigorosamente definita come limite del rapporto incrementale, provando poi i vari teoremi del calcolo.

|    un passo da Lagrange    |    e uno da Bolzano    |    il limite in Cauchy    |   

Un passo dalla Théorie des fonctions analytiques di Lagrange.

Il punto di partenza nella costruzione teorica di Lagrange è lo sviluppo in serie di una qualsiasi funzione $f(x)$, dove egli per funzione di una o più quantità intende ``ogni espressione del calcolo nella quale queste quantità entrano in maniera qualunque, insieme o no con altre quantità che si considerano come aventi dei valori dati e costanti, mentre le quantità della funzione possono assumere ogni valore possibile''. La serie ottenuta sostituendo $x+i$ al posto di $x$ sarà una serie di potenze in cui ``non si può trovare nessuna potenza frazionaria di $i$''. Essendosi assicurato della forma generale dello sviluppo di ogni funzione, Lagrange studia il significato di ogni termine, ricavando in particolare dallo sviluppo le funzioni ``derivate''.

* Pagina in mostra VI. 1

Joseph Louis Lagrange
Théorie des fonctions analytiques
Dopo queste considerazioni generali sullo sviluppo delle funzioni, consideriamo in particolare la formula

\begin{displaymath}f(x+i)=f(x)+pi+qi^2+ri^3+\mbox{ecc.}\end{displaymath}

e cerchiamo come queste funzioni derivate $p$, $q$, $r$, ecc. dipendono dalla funzione primitiva $f(x)$.
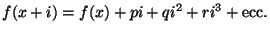
Per questo supponiamo che l'indeterminata $x$ diventi $x+o$, $o$ essendo una quantità qualunque indeterminata e indipendente da $i$; si vede che $f(x+i)$ diventerà $f(x+i+o)$ e si vede al tempo stesso che si avrà lo stesso risultato ponendo semplicemente $i+o$ al posto di $i$ in $f(x+i)$. Dunque il risultato dovrà essere lo stesso, sia ponendo nella serie $f(x+i)=f(x)+pi+qi^2+ri^3+\mbox{ecc.}$ $i+o$ al posto di $i$, sia ponendo $x+o$ al posto di $x$. [...]
torna a inizio pagina

Un passo dal Rein analitischer Beweis des Lehrsatzes di Bolzano.

* Pagina in mostra VI.2

Bernard Bolzano
Rein analytischer Beweis des Lehrsatzes
Se in una successione di grandezze $F_1(x)$, $F_2(x)$, $F_3(x)$, ..., $F_n(x)$, ..., $F_{n+r}(x)$, la differenza tra il termine ennesimo $F_n(x)$ e ogni termine successivo $F_{n+r}(x)$, lontano quanto si vuole dall'ennesimo, si mantiene più piccola di ogni grandezza data, prendendo $n$ sufficientemente grande, allora esiste sempre una certa grandezza costante ed una sola a cui si avvicinano sempre più i termini di questa successione e a cui si possono avvicinare tanto quanto si vuole prolungando la serie sufficientemente lontano.
torna a inizio pagina

Il limite in Cauchy.

Nell'introduzione del Cours d'analyse Cauchy critica il ricorso a ``ragionamenti tratti dalla generalità dell'algebra'', in implicita polemica con Lagrange. Dice infatti:
Ragionamenti di questo tipo, benché ammessi abbastanza comunemente, soprattutto nel passaggio dalle serie convergenti alle serie divergenti e dalle quantità reali alle espressioni immaginarie, non possono essere considerati, mi sembra, che come delle induzioni adatte a far talvolta presentire la verità, ma che poco si accordano con l'esattezza tanto vantata dalle scienze matematiche. Bisogna inoltre osservare che essi tendono a far attribuire alle formule algebriche un'estensione indefinita, mentre in realtà la maggior parte di queste formule sussiste unicamente sotto certe condizioni e per certi valori delle quantità in esse contenute [...] Così, prima di effettuare la somma di una qualunque serie, ho dovuto esaminare in quali casi le serie possono essere sommate o, in altri termini, quali sono le condizioni della loro convergenza; e, su questo argomento, ho stabilito delle regole generali, che mi sembrano meritare qualche attenzione.
Come già detto, il punto fondamentale della costruzione di Cauchy diviene la definizione di limite.

* Pagina in mostra VI.3

Augustin Luis Cauchy
Cours d'analyse
Allorché i valori successivamente assunti da una stessa variabile si avvicinano indefinitamente a un valore fissato, in modo da finire per differirne di tanto poco quanto si vorrà, quest'ultimo è chiamato il limite di tutti gli altri. Così ad esempio un numero irrazionale è il limite delle diverse frazioni che ne forniscono valori sempre più approssimati. In geometria la superficie di un cerchio è il limite verso il quale convergono le superfici dei poligoni inscritti, mentre il numero dei loro lati cresce sempre di più, ecc. Allorché i successivi valori numerici di una stessa variabile decrescono indefinitamente in modo da diventare minori di un numero dato, questa variabile diviene ciò che si chiama un infinitesimo o una quantità infinitesima. Una variabile di questo tipo ha zero come limite.
torna a inizio pagina

Storia del calcolo...

Indice della guida

Pagina successiva

Pagina principale