% Il metodo dei massimi e minimi di Fermat
 Il giardino di Archimede
 Un museo per la matematica

La geometria analitica e il problema delle tangenti


|   il metodo dei massimi e minimi di Fermat    |    il metodo di Descartes: dalla Géométrie - dai commenti di van Schooten    |    la costruzione cinematica di Roberval    |   

Il metodo dei massimi e minimi di Fermat

Nel gennaio del 1638, subito dopo la pubblicazione della Géométrie di Descartes, Pierre Fermat scrive una lettera a Mersenne, corrispondente di molti scienziati dell'epoca e tramite fondamentale per la diffusione di nuovi risultati, in cui espone un suo metodo per trovare i massimi e i minimi. Osservando che la differenza tra una curva e la sua tangente ha nel punto di tangenza un minimo (o un massimo), di tale metodo egli si serve per la determinazione delle tangenti ad una curva. Il metodo di Fermat prescrive di considerare l'espressione data nell'incognita $A$ e l'espressione stessa in cui l'incognita è sostituita dalla quantità $A+E$. Per $E=0$ le due espressioni coincideranno in un massimo (o un minimo). Partendo allora da un'espressione polinomiale, dopo aver uguagliato, anzi ``adeguagliato'', le due espressioni, svolto ed eliminato i termini comuni si divide per $E$ (o per la potenza minima con cui $E$ compare) l'espressione rimasta, che avrà termini contenenti $E$ o sue potenze, e infine si eliminano i termini che contengono ancora $E$. Dall'equazione così ottenuta si ricava poi il valore cercato per $A$. Non è difficile vedere che il procedimento descritto corrisponde ai seguenti passaggi tradotti in notazione moderna. Se indichiamo con $F(A)=0$ l'equazione di partenza, si ha:
i)
$F(A)-F(A+E)=0$
ii)
$\frac{F(A)-F(A+E)}{E}=0$
iii)
$\frac{F(A)-F(A+E)}{E}\vert _{E=0}=0$
Si noti l'affinità del passaggio finale con la nostra equazione $F'(A)=0$ soddisfatta dai punti di massimo o minimo interni. Mentre però quest'ultima è ottenuta facendo il limite per $E\rightarrow 0$, la iii) si ottiene ponendo $E=0$ nella ii). Nel caso in cui $F$ sia un polinomio i due procedimenti portano allo stesso risultato, ma in generale non sarà possibile dividere per $E$ e poi porre $E=0$. Basta che nell'equazione iniziale compaiano nelle radici perché il procedimento si complichi e divenga inservibile. Proprio annunciando il superamento del problema della manipolazione di quantità più complesse come quelle irrazionali Leibniz pubblicherà la sua Nova methodus, che segna l'inzio del calcolo differenziale. Il metodo dei massimi e minimi viene usato da Fermat per la determinazione delle tangenti osservando che la differenza tra una curva e la sua tangente ha nel punto di tangenza un minimo (o un massimo) (vedi oltre), ma trova anche altre applicazioni. Scrive Fermat:
Il metodo non fallisce mai e può essere esteso a un gran numero di questioni molto belle; per mezzo di esso abbiamo infatti trovato il centro di gravità di figure limitate da linee curve e rette, di solidi e molte altre cose delle quali tratterò un'altra volta, se avremo il tempo.
La prima pubblicazione a stampa del metodo si ha nel quinto volume del Supplementum Cursus Mathematici (1642) scritto da Herigone e solo nel 1679 appare nei Varia opera mathematica di Fermat come Methodus ad disquirendam maximam et minima, seguito dal De tangentibus linearum curvarum.

* Pagina in mostra II.1

Pierre de Fermat
De tangentibus linearum curvarum
Sia data per esempio la parabola BDN, di vertice D e diametro DC e il punto B su di essa, per il quale si deve condurre la retta BE, che è tangente alla parabola e interseca il diametro nel punto E [...].
Per determinare la tangente in B alla parabola, si determina, come d'uso a quel tempo, la sottotangente, ossia il segmento CE. Fermat, usando il metodo dei massimi e minimi, prova che deve essere CE=2CD. Per far ciò egli osserva che per le proprietà della parabola $CD:DI>BC^2:OI^2$, poiché il punto O è esterno alla parabola. Da qui, per la similitudine dei triangoli BCE e OIE, si ha $CD:DI>CE^2:IE^2$. Indicando allora con D la quantità data CD, con A quantità incognita CE e con E la ``variazione'' CI, si ha $D:(D-E)>A^2:(A-E)^2$. Si prosegue ora come descritto nel procedimento generale per la determinazione dei massimi e minimi: i) l'equazione ottenuta ``adeguagliando'' i due termini della disequazione, viene svolta e semplificata eliminando i termini uguali a destra e sinistra, ii) si divide tutto per E, iii) si eliminano i termini contenenti ancora E. In questo modo si perviene all'equazione $A^2=2AD$, da cui $A=2D$, cioè $4CE=2CD$.
torna a inizio pagina

Il metodo di Descartes

Il metodo seguito da Descartes nella Géométrie per determinare la tangente a una curva è più analitico-algebrico. Il problema si trova qui sotto la forma equivalente di determinare la normale in un punto alla curva data. Si considera allora un cerchio di centro variabile su uno degli assi e si impone la condizione algebrica che il cerchio abbia due intersezioni coincidenti con la curva nel punto. Il metodo viene prima spiegato in generale e poi applicato per esempio all'ellisse e alla parabola di Descartes.

* Pagina in mostra II.2

René Descartes
Géométrie
Sia CE la curva e per il punto C occorra tracciare una retta che formi con essa angoli retti. Suppongo tutto già compiuto e assumo CP come linea cercata, linea che prolungo fino a P dove incontra la retta GA, che suppongo essere quella a cui debbono riferirsi tutti i punti della linea CE. Così ponendo MA o CB = y, CM o BA = x, otterrò una certa equazione che esprime la relazione che sussiste tra x e y. [...]
Con un linguaggio e un formalismo per noi familiare, Descartes prosegue spiegando che se si pone per il cerchio incognito PC=s e PA=v, osservando che il triangolo PMC è rettangolo, si ha $s^2=x^2+v^2-2vy+y^2$, da cui si può ricavare la x (o equivalentemente la y) e sostituirla nell'equazione della curva data. Poi,
``dopo aver trovato [tale equazione] invece di servircene per conoscere le quantità x o y [...] che sono già date poiché il punto C [nel quale dobbiamo determinare la normale alla curva] è dato, dobbiamo usarla per trovare v o s che determinano il punto P richiesto [centro del cerchio cercato]. A tal fine bisogna considerare che se questo punto P è come lo desideriamo il cerchio di cui sarà il centro e che passerà per C vi toccherà la curva CE senza intersecarla. Al contrario se P è un po' più vicino o un po' più lontano dal punto A di quel che deve essere, il cerchio intersecherà la curva non solo nel punto C ma necessariamente anche in qualche altro [E]. [...] però tanto più questi due punti, C ed E, saranno vicini, tanto minore è la differenza che sussiste tra le radici [dell'equazione]. Infine se questi punti giacciono ambedue in uno (cioè se il cerchio che passa per C vi tocca la curva senza intersecarla) queste radici saranno assolutamente uguali [...].''
Dunque basterà imporre che il polinomio abbia due radici doppie. Se l'equazione della curva era di grado $m$ il polinomio risultante avrà grado $2m$ e sarà della forma $(y-y_0)^2Q(y)$ dove $Q(y)$ è un generico polinomio di grado $2(m-1)$. Uguagliando i coefficienti delle potenze omologhe si ottengono $2m+1$ equazioni dalle quali si possono ricavare i $2m-1$ coefficienti di $Q$ nonché i parametri v ed s.
torna a inizio pagina

La Géométrie si diffonde tra i matematici principalmente attraverso le due edizioni latine curate da Franz van Schooten. La prima viene pubblicata nel 1649 e oltre alla traduzione della Géométrie contiene le Notae breves di De Beaune e i Commentarii di Schooten. Nella seconda edizione, in due volumi, si aggiungono vari altri opuscoli, tra cui due lettere di John Hudde contenenti un teorema sulle radici doppie che porta a una semplificazione del procedimento precedente. I commenti di Schooten coprono tutti e tre i libri della Géométrie con puntuali note, osservazioni, integrazioni ed applicazioni. Per quanto riguarda il problema delle tangenti, Schooten illustra come applicare il metodo di Descartes in vari esempi, tra cui la determinazione della normale alla concoide.

* Pagina in mostra II.3




Franz van Schooten
In geometriam Renati Des Cartes Commentarii
Sia CE la prima concoide degli antichi, di polo G e di direttrice AB, tale che tutti i segmenti i cui prolungamenti si intersecano in G e sono compresi tra la curva CE e la retta AB, (come AE, LC) siano uguali. Si chiede di tracciare una linea retta (come CP), che intersechi la detta concoide ad angolo retto in un dato punto C. [...] Bisogna dunque soltanto prendere sulla retta CG il segmento CD uguale a CB, che è perpendicolare ad AB, e poi dal punto D condurre DF parallela ad AG ed uguale a GL; e si avrà in questo modo il punto F, per il quale si dovrà tracciare la linea richiesta CP.
[segue la costruzione con il metodo di Descartes]
torna a inizio pagina

La costruzione cinematica delle tangenti

Nel 1644 Mersenne rende noto un metodo per costruire le tangenti ad una curva, comunicatogli da Gilles Personne de Roberval, professore al College Royal di Parigi. Nello stesso anno Torricelli pubblica un metodo analogo nelle sue Opera geometrica. Entrambi i metodi presuppongono che sia nota la scomposizione cinematica della curva a cui si vuole tracciare la tangente: nella parabola, per esempio, un punto si allontana dal fuoco con la stessa velocità con cui si allontana dalla direttrice, nell'ellisse si avvicina a un fuoco con la stessa velocità con cui si allontana dall'altro, nella spirale un punto ruota intorno all'origine con la stessa velocità con cui se ne allontana, fatto già noto ed utilizzato da Archimede. Il manoscritto di Roberval, redatto da un suo allievo, fu presentato nel 1668 all'Académie des Sciences e pubblicato in una raccolta di scritti solo nel 1693. L'``assioma o principio d'invenzione'' che sta alla base del metodo è che ``la direzione del movimento di un punto che descrive una linea curva è la tangente alla linea curva in ogni posizione di quel punto'', principio ``abbastanza intellegibile'' che ``si accetterà facilmente se lo si sarà considerato con un po' di attenzione''. Da qui discende la ``regola generale'' da seguire per il tracciamento delle tangenti:
Per le proprietà specifiche della linea curva (che vi saranno date) esaminate i diversi movimenti che il punto che la descrive ha nel posto dove voi volete tracciare la tangente: componete tutti questi movimenti in uno solo, tracciate la linea della direzione del movimento composto e avrete la tangente della linea curva.
Applicando ``parola per parola'' la regola si studiano varie curve:
le tangenti alle sezioni coniche, le tangenti alle altre principali curve conosciute dagli antichi e ad alcune curve descritte recentemente, come la lumaca del signor Pascal, la cicloide del signor Roberval, la parabola di secondo genere del signor Descartes, ecc.
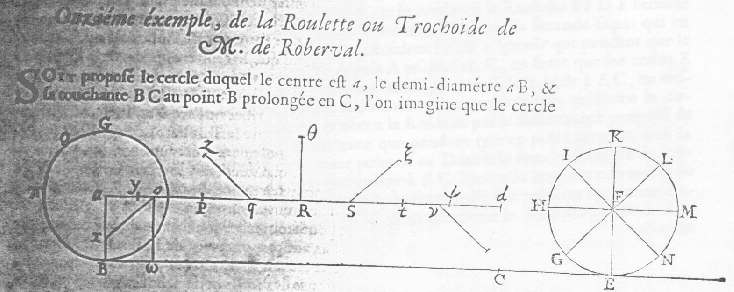L'undicesimo esempio dell'opuscolo riguarda appunto la cicloide che Roberval chiama ``roulette'' o ``trochoïde''. La curva è tracciata da un punto B che si trova su una circonferenza quando questa rotola su una retta BC. Un altro modo per generare la curva è considerare che la circonferenza trasli di moto uniforme in modo che il centro a descriva il segmento di base ad e nello stesso tempo il punto B percorra uniformemente la circonferenza. Nel caso in cui la lunghezza della base sia uguale a quella della circonferenza si ha una roulette di prima specie, ma più in generale si possono considerare i casi in cui la base sia più lunga o più corta della circonferenza. Dopo aver descritto la costruzione per punti della curva, Roberval descrive la costruzione della tangente in un punto E qualsiasi sulla base della scomposizione nei due moti simultanei.

* Pagina in mostra II.4

Gilles Personne de Roberval
Observations sur la composition des mouvements et sur le moyen de trouver les touchantes des lignes courbes.
Sia data dunque la roulette ABC di base ADC, vertice B e asse BD; se ne chiede la tangente nel punto E. Descrivere il cerchio BDF della roulette [...]; dal punto E tirare la retta EF parallela ad AC che interseca in F la circonferenza del semicerchio della roulette [...]; tracciare FG tangente al cerchio, poi prendere H sulla tangente del cerchio in modo tale che AC sta alla circonferenza del cerchio come EF sta a FH; dal punto H tracciare HE, e questa sarà la tangente alla roulette.
La costruzione di Roberval viene poi messa a confronto con quella data da Fermat:
``si traccia EF come sopra; si traccia la retta FB e per il punto E si traccia AH parallela a FB. EH sarà la tangente''.
Si prova che le due costruzioni sono in accordo ma, si dice, il metodo di Fermat non è così generale poiché funziona solo per la cicloide di prima specie.
torna a inizio pagina


Storia del calcolo...

Indice della guida

Pagina successiva

Pagina principale