
In ogni caso, non abbiamo né un enunciato preciso del teorema, né tanto meno una sua dimostrazione.
 |
La prima testimonianza nota
relativa al teorema di Pitagora è contenuta in una tavoletta paleobabilonese, databile
tra il 1800 e il 1600 a. C., in cui è disegnato un quadrato con le due diagonali. Il lato
del quadrato porta il numero 30, lungo la diagonale troviamo i numeri (in notazione
sessagesimale) 1;24,51,10, cioè 1+24/60+51/602+10/603 ,e 42;25,35,
ovvero 42+25/60+35/602 , che riportati in forma decimale danno 1,414213 e
42,42639. Il primo è un’ottima approssimazione della radice di 2; il secondo è la
diagonale del quadrato di lato 30, ed è uguale al prodotto di 30 per il primo numero. Il
fatto che la diagonale del quadrato si ottenga moltiplicando il suo lato per la radice di
2 denota la conoscenza del teorema di Pitagora, almeno nel caso del triangolo con i cateti
uguali. |
| Più dubbie le altre attribuzioni. Quella
più volte ripetuta, secondo la quale i geometri egizi, per trovare un angolo retto, si
servivano di una corda con segnati tratti di lunghezza 3, 4 e 5, che formano i lati di un
triangolo rettangolo, sembra sprovvista di ogni fondamento, e semmai ha a che fare con
l’inverso del teorema di Pitagora (vedi scheda). |

|
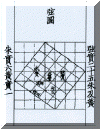
Anche la figura cinese
"hsuan-thu", che risale forse (ma la datazione è incerta) al 1200 a. C., è
stata vista da alcuni come una prova della conoscenza del teorema di Pitagora, ma questa
affermazione è controversa. In effetti la figura mostra un triangolo di lati 3, 4 e 5,
con il quadrato di lato 7=3+4 che contiene quello di lato 5, a sua volta composto da
quattro triangoli e un quadratino di lato 1=4-3. Non c’è invece traccia dei quadrati
sui cateti 3 e 4. In generale, se si indicano con a e b i cateti e con c
l’ipotenusa, il quadrato di lato a + b si può considerare composto di 8
triangoli e del quadratino di lato b - a, o anche del quadrato sull’ipotenusa c
e di quattro triangoli, da cui si ricava la relazione
4ab+ (b - a) 2 =
c2 +2ab.
Sviluppando (b - a)2
= b2 + a2 –2ab, si ottiene
b2 + a2 = c2
e quindi il teorema di Pitagora, purché
si conosca la formula del quadrato del binomio (b - a)2 =b2
+ a2 –2ab. Inutile dire che quest’ultima formula,
specie nella sua versione geometrica che qui sembra necessaria, non è per nulla più
facile del teorema di Pitagora che si vuole dimostrare.
In ogni caso, non abbiamo né un enunciato preciso del teorema, né tanto meno una sua dimostrazione. |