Un'altra dimostrazione semplicissima.

	La parte bianca insieme ai due triangoli gialli forma il quadrato dell’ipotenusa, mentre insieme ai due triangoli verdi, uguali ai precedenti, dà i quadrati dei cateti. Naturalmente, anche qui l’evidenza visiva deve essere accompagnata da una dimostrazione, che ognuno può fare da sé.
	Sembra che la dimostrazione precedente sia stata trovata da G. B. Airy, astronomo dell’osservatorio di Greenwich dal 1836 al 1881, intorno al 1855. Nella parte bianca della figura, Airy scrisse la poesiola che segue: I am, as you may see, a2 + b2 – ab. When two triangles on me stand, Square of hypothenuse is plann’d; But if I stand on them instead, The squares of both sides are read. la cui traduzione può essere: Mi presento, signori, eccomi qui: a2 + b2 – ab. Con due triangoli sopra, chiedo scusa* Ecco il quadrato dell’ipotenusa. Ma se questi di sotto stanno quieti Si formano i quadrati dei cateti. *Di "chiedo scusa", amici, chiedo scusa, non ho la rima dell’ipotenusa ...
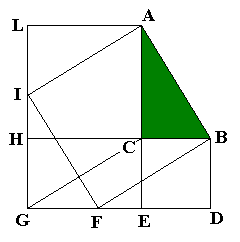
	La dimostrazione di Thabit Ibn Qurra. La dimostrazione seguente è attribuita al matematico arabo Thabit Ibn Qurra (826-901). A partire dal triangolo rettangolo ABC costruiamo il poligono irregolare ABDGLA aggiungendo al triangolo i quadrati  sui cateti ALHC e CBDE e il rettangolo HCEG. Quest’ultimo è diviso dalla diagonale GC in due triangoli rettangoli, uguali al triangolo ABC. Prendiamo ora LI uguale a BC e FD uguale ad AC; anche i triangoli rettangoli ALI e BFD sono uguali ad ABC. Lo stesso è vero per il triangolo IGF, perché si ha GI=AC e GF=BC. Infine, il quadrilatero AIFB ha tutti i lati uguali e l’angolo IAB è retto, essendo uguale all’angolo LAC (gli angoli LAI e CAB sono uguali e l’angolo IAC è comune); dunque AIFB è il quadrato costruito sull’ipotenusa AB. A questo punto la dimostrazione è immediata. Infatti il poligono irregolare ABDGLA si può scomporre sia nei due quadrati sui cateti e nei tre triangoli uguali ABD, HCG e GCE, sia nel quadrato sull’ipotenusa e nei tre triangoli (uguali ai primi) FBD, IFG e ILA.