Un triangolo non rettangolo

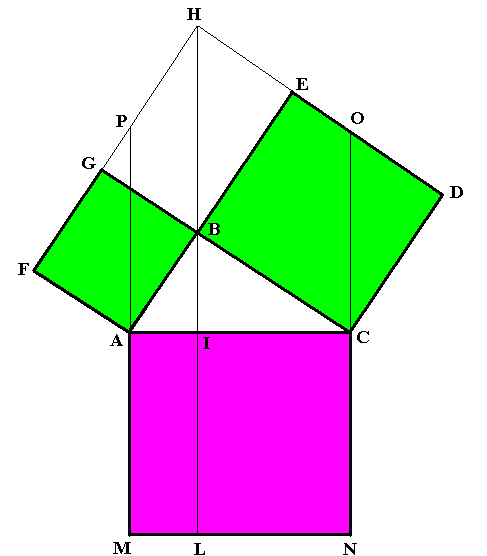
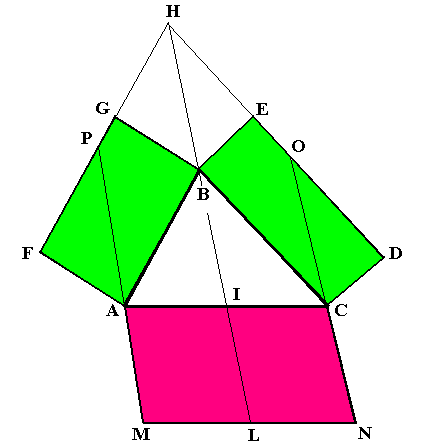
Nella Collezione Matematica di Pappo, un matematico greco del V secolo d. C., troviamo la seguente costruzione, valida anche se il triangolo ABC non è rettangolo. Su due lati AB e BC costruiamo due parallelogrammi BCDE e ABFG, i cui lati DE e FG, prolungati, si incontrino nel punto H. Tiriamo la retta HB, e preso il segmento IL uguale ad HB, costruiamo il parallelogramma ACMN, con i lati AM e CN paralleli a IL. Questo parallelogramma è uguale alla somma di BCDE e AFGB. Per dimostrarlo, prolunghiamo i lati CN e AM. Il parallelogramma BCDE è uguale a BCOH, dato che hanno la stessa base BC e stanno tra le parallele BC e HD. Per lo stesso motivo BCOH è uguale a ICNL, dato che la base HB è uguale a IL per costruzione, e stanno tra le parallele HL e OC. Di conseguenza, i parallelogrammi BCDE e ICNL sono uguali. Analogamente, sono uguali AFGB e AILM, e dunque la somma di BCDE e AFGB è uguale a ACML.

Questo risultato contiene come caso particolare il teorema di Pitagora. Infatti se l’angolo in B è retto, e BCDE e AFGB sono due quadrati, il segmento HB, e dunque IL, è uguale all’ipotenusa AC (dato che GBEH è un rettangolo con i lati uguali ai cateti), e la retta HL è perpendicolare ad AC, per cui il parallelogramma ACNM è il quadrato dell’ipotenusa.