Parallelogrammi e trapezi

	Il teorema di Pitagora si può enunciare anche in una forma un po’ diversa: La somma dei quadrati della base e dell’altezza di un rettangolo è uguale al quadrato della diagonale. Infatti la diagonale di un rettangolo è l’ipotenusa del triangolo rettangolo che ha come cateti la base e l’altezza. Se poi prendiamo ogni quadrato due volte, avremo che: La somma dei quadrati dei lati di un rettangolo è uguale alla somma dei quadrati delle diagonali.
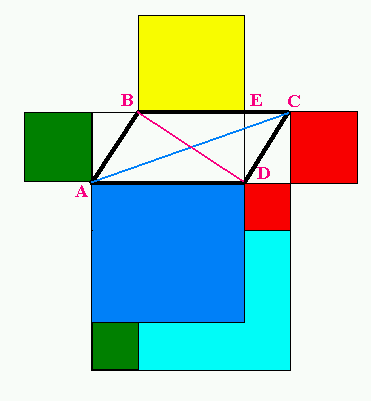
	Lo stesso risultato vale anche per un parallelogramma non rettangolo. Consideriamo il parallelogramma ABCD. Per il teorema di Pitagora applicato al triangolo rettangolo BED, il quadrato della diagonale BD è uguale alla somma dei quadrati di ED e di BE, colorati in verde e giallo. Analogamente, il quadrato della diagonale AC è uguale al quadrato rosso più quello multicolore. La somma delle aree dei quadrati delle diagonali è allora uguale a quella delle aree dei quattro quadrati disegnati nella prima figura. 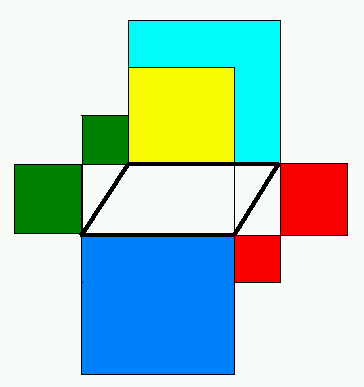La seconda figura è ottenuta dalla prima spostando alcuni pezzi senza cambiare l’area complessiva, e quindi la somma delle aree dei quattro quadrati della prima figura (che era uguale alla somma dei quadrati delle diagonali) è uguale a quella dei sei quadrati della seconda. D’altra parte, sempre per il teorema di Pitagora, i due quadrati verdi sono uguali al quadrato del lato AB, e i due rossi al quadrato del lato AC, e dunque la somma delle aree dei sei quadrati è uguale a quella dei quadrati dei lati. Possiamo allora concludere che: In un parallelogramma la somma delle aree dei quadrati delle diagonali è uguale alla somma delle aree dei quadrati dei quattro lati.
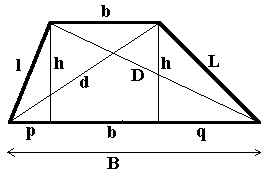
	Un risultato simile vale anche per i trapezi: La somma delle aree dei quadrati dei lati è uguale alla somma delle aree dei quadrati delle diagonali, più il quadrato della differenza tra la base maggiore e la minore. In questo caso la migliore dimostrazione è quella per via algebrica. Riferendoci alla figura che segue dobbiamo dimostrare che: L2 + l2 + B2 + b2 = D2 + d2 + (B - b)2. Cominciamo applicando il teorema di Pitagora ai triangoli di lati h, q, L e h, p, l. Si ha: h2 + q2 =L2 h2 + p2 = l2 Analogamente, applicando il teorema di Pitagora ai triangoli di lati h, D, b + q e h, d, b + p, risulta: D2 = (b + q)2 + h2 = b2 +q2 + 2bq + h2 = b2 +L2 + 2bq d2 = (b + p)2 + h2 = b2 +p2 + 2bp + h2 = b2 +l2 + 2bp e sommando D2 + d2 = L2 + l2 + 2b (b + p+ q) = L2 + l2 + 2bB. Osserviamo per inciso che quest’ultima formula, tradotta in termini geometrici, dice che: In un trapezio, la somma dei quadrati delle diagonali è uguale alla somma dei quadrati dei lati non paralleli, più due volte il rettangolo delle basi. Per arrivare al risultato voluto, facciamo uso della formula (B - b)2 = B2 + b2 – 2Bb, ossia 2Bb = B2 + b2 – (B - b)2 , che introdotta nella precedente, dà D2 + d2 = L2 + l2 + B2 + b2 – (B - b)2 , che è quello che si voleva dimostrare.
	Nel caso di un trapezio rettangolo, si può dare una rappresentazione visiva molto semplice. Nella figura che segue, applicando il teorema di Pitagora ai triangoli ABC ed ABD, abbiamo che la somma dei quadrati delle diagonali è uguale ai quattro quadrati disegnati. Di questi, i tre gialli sono i quadrati dei lati rispettivi, mentre il quadrato del lato CD si ottiene aggiungendo a quello verde il quadrato di DE, cioè della differenza delle basi. 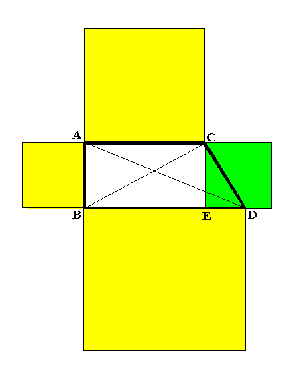Se dunque ai quadrati delle diagonali si aggiunge quello della differenza delle basi, si ottiene la somma dei quadrati dei lati.