La diagonale del
quadrato e gli irrazionali.
Una
delle scoperte
più importanti della scuola pitagorica è senza dubbio quella
dell’incommensurabilità del lato e della diagonale del quadrato.
Due segmenti L
e D sono commensurabili quando hanno un sottomultiplo comune, cioè quando L
e D sono multipli di uno stesso segmento H:
L = m H
D = n H
con m e n
interi.
I pitagorici
scoprirono che se L è il lato e D la diagonale di un quadrato, questa
relazione è impossibile. Quale fosse il loro ragionamento non si sa; tra quelli proposti,
due sembrano particolarmente semplici, uno più geometrico, l’altro algebrico.
Il
primo si basa sul
fatto che se due segmenti L e D sono commensurabili, e L<D<2L,
allora sono commensurabili anche D–L e 2L–D. Infatti si ha
D – L = (n – m) H
e
2L – D = (2m – n) H
e quindi anche D–L
e 2L–D hanno H come sottomultiplo.
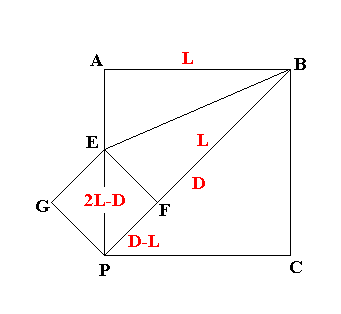 Supponiamo
ora per assurdo che il lato L e la diagonale D di un quadrato siano
commensurabili, e sia H un sottomultiplo comune. Dividiamo in due parti uguali
l’angolo ABP, e dal punto E tiriamo la perpendicolare EF
alla diagonale. I due triangoli ABE e BEF sono uguali (sono rettangoli,
hanno gli angoli in B uguali, e il lato BE comune); quindi BF=AB=L,
e PF=D-L. Il triangolo PEF è isoscele (infatti l’angolo EPF
è di 45 gradi), e dunque si ha AE=EF=FP=D-L, ed EP=L–(D–L)=2L-D.
Supponiamo
ora per assurdo che il lato L e la diagonale D di un quadrato siano
commensurabili, e sia H un sottomultiplo comune. Dividiamo in due parti uguali
l’angolo ABP, e dal punto E tiriamo la perpendicolare EF
alla diagonale. I due triangoli ABE e BEF sono uguali (sono rettangoli,
hanno gli angoli in B uguali, e il lato BE comune); quindi BF=AB=L,
e PF=D-L. Il triangolo PEF è isoscele (infatti l’angolo EPF
è di 45 gradi), e dunque si ha AE=EF=FP=D-L, ed EP=L–(D–L)=2L-D.
Completiamo il
quadrato EFPG. Siccome avevamo supposto che il lato L e la diagonale D
avessero un comune sottomultiplo H, anche il lato PF=D–L e la
diagonale EP=2L–D del quadrato piccolo avranno lo stesso sottomultiplo H.
Se ripetiamo in
questo quadrato la costruzione che abbiamo fatto nel precedente, otteniamo un nuovo
quadrato, ancora più piccolo, il cui lato e la cui diagonale hanno ancora H come
sottomultiplo. Continuando sempre nello stesso modo, otteniamo dei quadrati sempre più
piccoli, tutti però con il lato e la diagonale che hanno H come sottomultiplo
comune.
Ma questo non è
possibile, perché il lato e la diagonale diventano sempre più piccoli, e dopo un certo
numero di passi finirebbero per diventare minori di H, cioè di un loro
sottomultiplo. Siamo dunque arrivati a un assurdo, e quindi il lato e la diagonale di un
quadrato non possono essere commensurabili.
Una seconda
dimostrazione, di tipo più algebrico, è probabilmente quella evocata da Aristotele
quando dice:
Una dimostrazione di questo tipo, ad esempio, è quella che stabilisce l'incommensurabilità
della diagonale [e del lato del quadrato], che si fonda sul fatto che se si suppone che
siano commensurabili, i numeri dispari risultano uguali ai numeri pari.
Per preparare il
campo, osserviamo che due lati consecutivi e la diagonale di un quadrato formano un
triangolo rettangolo, e quindi si ha
D2
= L2 + L2 = 2 L2.
Supponiamo ora che D
e L siano commensurabili, e cioè che risulti L=mH e D=nH. Si
avrebbe allora
n2
H2 = 2 m2 H2
e quindi
n2
= 2 m2.
Nell’equazione
precedente possiamo eliminare tutti i fattori comuni a m e a n (se ce ne
sono), e quindi possiamo supporre che m e n siano primi tra loro, cioè
non abbiano fattori comuni. In particolare, non possono essere ambedue pari.
Osserviamo ora che n2
è pari (dato che è uguale a 2m2 che è pari), e quindi n è
pari e m è dispari. Si può allora scrivere n=2p, e pertanto, essendo n2=4p2
, dall’equazione precedente si ricava 4p2=2m 2 , e,
dividendo per 2:
2 p2
= m 2.
Ragionando come
sopra, avremo allora che m2 è pari, e dunque anche m è
pari. Questo è assurdo, perché m era dispari.
Possiamo rivedere
questo risultato da un punto di vista leggermente diverso, osservando che abbiamo
dimostrato che l’equazione
n2
= 2 m2
non ha nessuna
soluzione in numeri interi, ovvero che non esistono due interi m e n
tali che n2/m2=2. Estraendo la radice quadrata, possiamo
concludere che non esiste nessuna frazione n/m uguale alla radice di 2.
I numeri che si
possono esprimere per mezzo di frazioni si chiamano razionali; quelli che non sono uguali
a nessuna frazione si dicono irrazionali. Possiamo allora affermare che radice di 2 è un
numero irrazionale.
Con un ragionamento
analogo si dimostra che sono irrazionali le radici di 3, di 5, e in genere di tutti gli
interi che non sono quadrati perfetti. In altre parole, la radice di un intero è o un
intero (come avviene ad esempio per 4 o 9) o un numero irrazionale.
 Supponiamo
ora per assurdo che il lato L e la diagonale D di un quadrato siano
commensurabili, e sia H un sottomultiplo comune. Dividiamo in due parti uguali
l’angolo ABP, e dal punto E tiriamo la perpendicolare EF
alla diagonale. I due triangoli ABE e BEF sono uguali (sono rettangoli,
hanno gli angoli in B uguali, e il lato BE comune); quindi BF=AB=L,
e PF=D-L. Il triangolo PEF è isoscele (infatti l’angolo EPF
è di 45 gradi), e dunque si ha AE=EF=FP=D-L, ed EP=L–(D–L)=2L-D.
Supponiamo
ora per assurdo che il lato L e la diagonale D di un quadrato siano
commensurabili, e sia H un sottomultiplo comune. Dividiamo in due parti uguali
l’angolo ABP, e dal punto E tiriamo la perpendicolare EF
alla diagonale. I due triangoli ABE e BEF sono uguali (sono rettangoli,
hanno gli angoli in B uguali, e il lato BE comune); quindi BF=AB=L,
e PF=D-L. Il triangolo PEF è isoscele (infatti l’angolo EPF
è di 45 gradi), e dunque si ha AE=EF=FP=D-L, ed EP=L–(D–L)=2L-D.