Terne pitagoriche

|    il viceversa del teorema di Pitagora    |    costruzione di triangoli rettangoli    |    terne pitagoriche    |    il teorema di Fermat    |   

Una delle tante formulazioni del teorema di Pitagora dice che se a e b sono i cateti di un triangolo rettangolo e c è l'ipotenusa, si ha a2 + b2 = c2.
Vale anche il viceversa:
Se i lati a, b e c di un triangolo verificano la relazione a2 + b2 =c2, allora il triangolo è rettangolo, a e b sono i cateti e c l'ipotenusa.

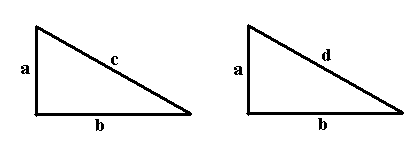scheda8.gif (2121 byte) La dimostrazione è molto semplice. Costruiamo un triangolo rettangolo con i cateti a e b, e sia d la sua ipotenusa. Per il teorema di Pitagora si ha d2 = a2 + b2, mentre per ipotesi a2 + b2 = c2. Ne deriva che d2 = c2, dunque d = c, cosicché i due triangoli hanno i tre lati uguali, e dunque sono uguali. Ma il secondo era per costruzione un triangolo rettangolo con i cateti a e b, e quindi lo stesso vale per il primo.

Il risultato precedente ci dà un metodo molto semplice per costruire triangoli rettangoli senza bisogno di misurare gli angoli. Infatti basta trovare tre numeri a, b e c, che verifichino la relazione a2 + b2 = c2; il triangolo di lati a, b e c sarà automaticamente rettangolo.
Un esempio è il triangolo di lati 3, 4 e 5; siccome 32+42=9+16=25=52, il triangolo con questi lati è rettangolo. Questo triangolo si trova spesso nei testi più antichi. Altri triangoli rettangoli sono quelli di lati 5, 12 e 13, oppure 8, 15 e 17.
Notiamo che i lati di tutti questi triangoli sono numeri interi. Per il teorema di Pitagora questo non è necessario; basta che sia verificata la relazione a2 + b2 = c2, come ad esempio nel triangolo che ha i cateti uguali a 1 e l’ipotenusa uguale a radice di 2. D'altra parte i triangoli con lati interi sono più interessanti, anche perché i loro lati debbono essere scelti con cura; ad esempio non se ne può scegliere uno a piacere e cercare poi gli altri due.

Se tre numeri a, b e c verificano la relazione a2+b2=c2 si dice che formano una terna pitagorica. Ad esempio 3, 4 e 5 sono una terna pitagorica, ma non 1, 1 e radice di 2, perché quest'ultimo numero non è intero.
Le terne pitagoriche sono tutte descritte dalla formula

a = m2 - n2

b = 2mn

c = m2 + n2

 (1)

dove m ed n sono due numeri interi, con m>n.
Che i numeri a, b e c formano una terna pitagorica, si verifica facilmente. Infatti si ha a2 = (m2 - n2)2 = m4 + n4 - 2m2 n2 e b2 = (2mn)2 = 4 m2 n2 e quindi a2 + b2 = m4 + n4 - 2m2 n2 + 4 m2 n2 = m4 + n4 + 2m2 n2 = (m2 + n2)2 = c2.
Più difficile è dimostrare che la formula (1) dà tutte le possibili terne pitagoriche, a meno di un fattore comune. Ecco come si può fare.
Cominciamo con l’osservare che se a, b e c formano una terna pitagorica, lo stesso vale per ha, hb e hc. Ci si può quindi limitare a considerare terne con a e b primi tra loro; tutte le altre si otterranno moltiplicando a, b e c per lo stesso numero.
Facciamo ora vedere che a e b devono essere uno pari e uno dispari, e di conseguenza c deve essere dispari.
Che a e b non siano ambedue pari dipende dal fatto che sono primi tra loro. Che non possano essere ambedue dispari, è un po’ più delicato.
Se a e b fossero dispari, lo sarebbero anche a2 e b2 , cosicché c2 , somma di due numeri dispari, sarebbe pari, e quindi c sarebbe pari. D’altra parte, se a e b sono dispari si deve avere
a = 2k+1 e b=2h+1, da cui a2 = (2k+1)2 = 4k2 +4k+1, b2 =4h2 +4h+1 e sommando si ottiene c2 =a2 +b2 = 4(k2 +k+h2 +h) + 2. Da questa formula segue che dividendo c2 per 4 si ottiene il quoziente k2 +k+h2 +h e il resto 2. In particolare, c2 non è divisibile per 4, e questo è assurdo, dato che c è pari.
Riassumendo, se a, b e c formano una terna pitagorica, i due numeri a e b devono essere uno pari e uno dispari (ad esempio b pari ed a dispari), e di conseguenza c deve essere dispari.
Nella relazione a2 +b2 = c2 portiamo a2 a secondo membro; si ha: b2 = c2 - a2 = (c + a)(c – a). Siccome a e c sono dispari, c+a e c–a sono pari. Se poniamo b=2s, c+a=2x e c–a=2y, avremo s2=xy. Anche x e y sono primi tra loro; infatti se avessero un fattore comune q, anche a = x – y sarebbe divisibile per q, e lo stesso sarebbe vero per b2 , e dunque per b, in contraddizione con l’ipotesi che a e b fossero primi tra loro. Siccome il prodotto xy è un quadrato, x e y sono essi stessi dei quadrati: x=m2 e y=n2 . Si avrà allora in conclusione: a=x–y=m2-n2; c=x+y=m2+n2 e b2=4xy=4m2n2 per cui b = 2mn.
La formula (1) è così dimostrata. Dando a m e n successivamente differenti valori, sempre primi tra loro, e uno pari e l’altro dispari, troviamo tutte le possibili terne pitagoriche.
Notiamo che quando n = m – 1, si ha anche b = c – 1, cosa che chi legge potrà dimostrare facilmente.

Dalla considerazione delle terne pitagoriche, Pierre Fermat (1601-1665) trasse lo spunto per cercare se fosse possibile trovare delle terne di numeri interi, tutti diversi da zero, che verificassero la relazione x3 + y3 = z3 o, più in generale, xn + yn = zn.
Nel margine della sua copia dell'Arithmetica di Diofanto, un autore greco vissuto intorno al III secolo d. C., al punto dove veniva spiegata la generazione delle terne pitagoriche, Fermat scrisse:

Cubem autem in duos cubos, aut quadratoquadratum in duos quadratoquadratos, et generaliter nullam in infinitum ultra quadratum potestatem in duos ejusdem nominis fas est dividere: cujus rei demonstrationem mirabilem sane detexi. Hanc marginis exiguitas non caparet.
cioè
Non è invece possibile dividere un cubo in due cubi. Un quadrato-quadrato in due quadrato-quadrati, e in genere nessuna potenza maggiore di due in due potenze dello stesso ordine. Di questo ho trovato una bellissima dimostrazione, che però non posso scrivere per la ristrettezza del margine.
Questo risultato, che è stato chiamato l'ultimo teorema di Fermat, ha stimolato le ricerche di molti tra i maggiori matematici degli ultimi tre secoli, ed è stato dimostrato totalmente solo nel 1994 da Andrew Wiles.