|
SCHEDE DI APPROFONDIMENTO
Il teorema di Pitagora nell'estrema antichità
Una dimostrazione semplice
Un'altra dimostrazione semplicissima
Un triangolo non rettangolo
Parallelogrammi e trapezi
Figure simili
La diagonale del quadrato e gli irrazionali
Terne pitagoriche
I solidi regolari
|
|
Una dimostrazione semplice
del teorema di Pitagora
|
Il
primo
enunciato preciso, e la prima dimostrazione inequivocabile del nostro teorema si trovano
nel primo libro degli Elementi di Euclide (circa 300 a. C):
Nei
triangoli rettangoli, il quadrato del lato opposto all’angolo retto è uguale ai
quadrati dei lati che contengono l’angolo retto.
Oggi in genere il
"lato opposto all’angolo retto" si chiama ipotenusa, mentre i
"lati che contengono l’angolo retto" prendono il nome di cateti.
Inoltre, invece di "uguale" si preferisce dire equivalente, o che ha la
stessa area. Così una formulazione moderna può essere:
Nei
triangoli rettangoli, l’area del quadrato costruito sull’ipotenusa è uguale
alla somma delle aree dei quadrati costruiti sui cateti.
o anche, dato che
l’area del quadrato è uguale al quadrato del lato,
Nei
triangoli rettangoli, il quadrato dell’ipotenusa è equivalente ai quadrati dei
cateti.
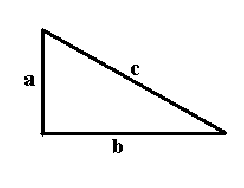
Se
si indicano questi ultimi con a e b, e l’ipotenusa con c, il
teorema prende la forma algebrica:
a2 +
b2 = c2
|

|
Tra
i teoremi
classici, quello che porta il nome di Pitagora è forse quello che ha avuto più
dimostrazioni differenti. Di tutte, la più semplice è probabilmente quella schematizzata
dalle figure a lato .
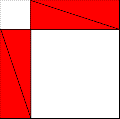
Il triangolo
rettangolo in questione è uno di quelli colorati in rosso. Il quadrato grande, che ha
come lato la somma dei cateti, nella prima figura è composto di quattro triangoli e dei
due quadrati costruiti sui cateti, mentre nella seconda è formato dagli stessi quattro
triangoli disposti diversamente, e del quadrato dell’ipotenusa. Siccome l’area
del quadrato grande e quella dei quattro triangoli è la stessa nei due casi, anche le
aree delle figure che restano (cioè nella prima dei quadrati costruiti sui cateti, e
nella seconda del quadrato sull’ipotenusa) sono uguali.
Come si vede, la
dimostrazione è molto facile, e soprattutto evidente: il risultato si vede prima ancora
di cominciare il ragionamento. Bisogna però stare molto attenti prima di accettare per
buona una dimostrazione visiva. A volte la vista può ingannare: quello che sembra un
quadrato può essere invece un rettangolo con i lati quasi uguali; due figure che sembrano
uguali in realtà differiscono, anche se di poco. Molti paradossi geometrici sono
costruiti in questo modo.
|
|
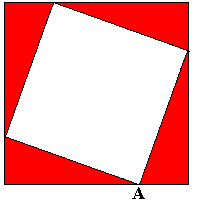
Nel
nostro caso, la
dimostrazione è corretta, ma non ancora completa. Occorre infatti dimostrare che le parti
bianche delle due figure sono effettivamente dei quadrati, e precisamente i quadrati sui
cateti nella prima e quello sull’ipotenusa nella seconda. Nella prima figura questo
è evidente per costruzione; nella seconda, il quadrilatero in esame ha tutti i lati
uguali all’ipotenusa, e dunque resta solo da far vedere che i suoi angoli sono retti.
Consideriamo ad esempio quello con il vertice nel punto A, che insieme ai due angoli rossi con lo
stesso vertice forma un angolo piatto. Ma anche la somma degli angoli di un triangolo è
uguale a un angolo piatto, e quindi l’angolo bianco col vertice in A è uguale al
terzo angolo del triangolo, che è retto. Allo stesso modo si dimostra che sono retti gli
altri angoli (a rigore questo non servirebbe, perché un rombo con un angolo retto è un
quadrato), e quindi la figura è un quadrato, che ha come lato l’ipotenusa.
|
|
|