|
A problem for which the cycloid represents the solution
is the determination of the so-called
brachistochrone.
This is the curve which reduces to the minimum the falling
time from one of its ends to the other. More precisely,
if we fix two points P and Q, the first higher
than the second but not on the vertical line, and let a body fall from
P to Q sliding on a curve which joins the two points, the problem now is:
among all the curves joining P to Q, which is the one that reduces
the falling time to the minimum? It isn't the straight line joining
the two points as one might suppose. In fact, in order
to reduce falling time it is expedient to start almost vertically,
so to gain speed straight away, even if the path is longer.
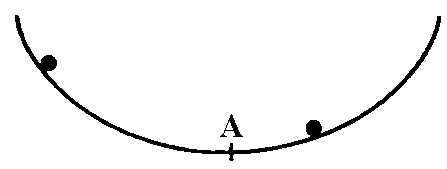
The exhibit shows that of two steel balls that left to fall simultaneously
from point A, one along a straight track and the other along a cycloidal,
the latter reaches point B first.
|