The Garden of Archimedes  A Museum for Mathematics

Newton and Leibniz: the birth of calculus

|    Liebniz's new method    |    Newton's method:     from the Principia    -     from the Methodus fluxionum    |   

Liebniz's new method

The title of the article published by Leibniz in 1684 on the Acta eruditorum can be translated as "New method for maxima and minima, and for tangents, that is not hindered by fractional or irrational quantities, and is the only method of calculus for these". The reference to Fermat's works highlights the much greater generality of the new method, as will shall see below.
The previous methods are limited by the need to use various means to simplify the equation, or better, the "adequation", $F(A)-F(A+E)=0$ before dividing by E and then putting $E=0$. The existence of roots or of complex fractions tends to block the way quite early on. The crucial point lies in the fact that considering the equation as a whole does not allow to solve difficulties separately by working out the simpler elements of the equation. In modern terms one could say that in order for this separation to become possible, it is necessary to make a distinction between the two moments, the one of the calculus of $F'$ and the other related to solving $F'=0$, In other words, there is a need to recognise the operational character typical of functional derivations.
This is one of the fundamental points both of the theory of Leibniz and of Newton. After accepting this observation, one can then proceed first with the calculus of the derivative, by using all the facilities offered by linearity and by the rules of differentiation of products and quotients, and then one can use that calculus to search for the maxima and minima or to determine the tangents.
The article of Leibniz starts in fact with the description of the rules of derivation. Before the notion of function was established, which happened only a few decades later, the concept that prevailed was that of a relation between variables that could be expressed in an equation $P(x,y)=0$. The issue of derivation therefore presents itself in this form: given a relation $P(x,y)=0$ between the variables x and y, find the relation between their differentials. In addition, since a clear concept of limit was not yet available at the time we are speaking of, the definition of the derivative took other paths and became based on intuitive observations which were later strongly attacked. In Leibniz, the derivative, or better, the differential, is defined through the tangent, avoiding all specific references to infinitesimal quantities (see below). This upturns the vision we are used to today. The rules thus expounded state that if $a$ is a constant quantity $da=0$ and $dax=adx$; $d(z-y+w+x)=dz-dy+dw+dx$, $dxy=dx+dy$ and finally, if z=v/y, $dz=\frac{(vdy-ydv)}{y^2}$.
In this way one can calculate the derivatives of first power and from these the derivatives of a root observing that if $z=x^{1/k}$, then $x=z^k$and, by differentiating , $dx=kz^{k-1}dz$,from which finally, $dz=\frac{1}{k}x^{\frac{1}{k}-1}dx$.
At this point, it becomes possible to differentiate any combination of powers and radicals, and thus any kind of function, since at that time, these combinations represented almost all the functions known. A good illustration of the different level of the new method compared to previous ones, was given by Leibniz in an example he chose as an application, consisting in a composition of fractions and radicals. The method is then used in another three typical examples: a problem of the minimum (determining the path of a refracted ray of light), a problem for the calculation of the tangent to a given curve, and the inverse problem of determining a curve starting from a given known subtangent.

In his elaboration, what Leibniz gives most of his attention to are the "differences" and in the Nova methodus he limits his exposition only to the presentation of the differential calculus, but as the correspondence with Newton demonstrates, Leibniz had already mastered, many years before, the inverse aspect which was the integral calculus.
To indicate the integral of a given differential$\omega$ he initially uses expressions such as $\mbox{omnia} \omega$ or $\mbox{omn} \omega$, inspired by Cavalieri. If $dy$ represents the infinitesimal increment of the variable $y$, the sum of these increments will recompose the $y$. Being very careful in the choice of the notations, he himself observes that to indicate the sum of the infinitesimal increments, it would be more convenient to use an oblong "s" that can serve to indicate the sum, in the same way $d$ indicates the difference.
Thus it can be said that $y=\int dy$ and if for example $dy=x^a$were true, then $y=\frac{x^{a+1}}{(a+1)}$, which occurs when differentiating.

* Exhibit III. 1

Gottfried Wilhelm Leibniz
Nova methodus pro maximis et minimis, itemque tangentibus, quae nec fractas nec irrationales quantitates moratur, et singulare pro illis calculi genus

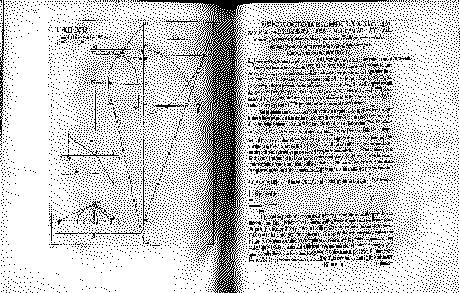
Given the axis AX and a set of curves such as VV, WW, YY, ZZ, and let VX, WX, YX, ZX be the ordinates of a point on the curves, perpendicular to the axis: the latter will be said v,w,y,z respectively; and let the segment AX, cut on the axis, be named x. Let the tangents be VB, WC, YD, ZE, meeting the axis respectively in the points B, C, D, E.
Now let any segment, choosen arbitrarily, be named dx and a segment that is to dx as v (or w, or y, or z) is to BX (or CX, or DX, or EX) be said dv (or dw or dy, or dz) which is the difference of those very v's (or of those w's, or y's, or z's).
Given that this is true, the rules will be:
if $a$ is a given constant quantity, then $da=0$ and $dax=adx$.
If y=v (that is if any ordinate of the curve YY is equal to any corresponding ordinate of the curve VV), then $dy=dv$.
Addition and subtraction :
if $z-y+w+x=v$, then $d(z-y+w+x)=dv=dz-dy+dw+dx$.
[...]

back to top

The method of Newton

Newton elaborated a similar theory to Leibniz some years before him, but he was only to publish it much later.
Unlike Leibniz who, in a certain sense, considered quantities as consisting of infinitesimal parts, Newton was interested in issues related to dynamics and motion in general.
Thus Newton considered quantities as variables in function of time: "flowing" quantities which have a given velocity and or "fluxion" at every instant.
Newton's infinitesimal calculus came out in three main editions: the first one is De analysi per aequationes numero terminorum infinitas, written in 1669 but published only later in 1711; the second is the one in which the typical notation of fluxions first appears, Methodus fluxionum et serierum infinitarum, edited in 1671 and published in 1742; the third is the one in which the method of the prime and ultimate ratios is expounded and appears in the De quadratura curvarum and is also used in Philosophiae naturalis principia mathematica the first works to be published.
In Newton, the derivative takes its role from the fluxion of a fluent quantity $y$, initially indicated with $p$ and then with $\dot{y}$, whilst the differential $dy$ corresponds to the "moment" $\dot{y}o$, outcome of the velocity multiplied by the infinitesimal interval of time $o$.
The fundamental problem of calculus is expressed in the following manner by Newton:

given a relation between flowing quantities, find the relation between their functions and vice-versa

a proposition which already appeared under the form of an anagram in a letter written to Leibniz in 1676. Thus for example, if $y=x^n$, Newton considers the moments $y+\dot{y}o$ and $x+\dot{x}o$, develops the second one with a binomial to the nth power, simplifies the terms not containing $o$, divides by $o$, ignores the terms still containing $o$ and obtains $y=nx^{n-1}\dot{x}$.
Fluxions, or better, moments of fluxions, are extracted by Newton also with the method of prime and ultimate ratios, that is in those relations in which the increment "disappears" (see below).
Newton dedicated more space than did Leibniz to the inverse issues of fluxions, and that is the search for quadratures, even though, as far as the notations are concerned, the ones made by Leibniz will prevail. What makes Newton's method differ from that of Leibniz is the skillful use he makes of developments in series. From the combination with the method of fluxions he gives birth to a very powerful tool, which he uses to solve the problem of integration by developing the integrated function and, as far as the differential equations are concerned, by generating a method of successive approximations capable of calculating the solution with the level of accuracy desired.

* Exhibit III. 2

Isaac Newton
Philosophiae naturalis Principia mathematica

Section I
Method of prime and ultimate ratios with which one can demonstrate the following
Lemma I
Quantities and relations between quantities tending constantly to equality in a given finite time and approaching each other before the time has expired more nearly than any given difference, become ultimately equal.
If this were not true they would be unequal in the end and D would be their final difference. Thus they will not tend to equality more than the given difference D. And this would be contrary to the hypothesis.

* Exhibit III. 3

Isaac Newton
Methodus fluxionum et serierum infinitarum

From now on I shall call these flowing quantities, which I shall consider gradually and indefinitely increasing and represent with the last letters of the alphabet u,y,x and z, so that they can be distinguished from the other quantities in equations, that are considered known and defined, and these are the ones indicated with the initial letters of the alphabet a, b, c, etc.
Velocities instead, of the flowing quantities increasing due to the movement that generates them (velocities which I call fluxions or simply velocities) are expressed with the same letters pointed, thus $\dot u$, $\dot y$, $\dot x$ and $\dot z$. In other words, for the velocity of the quantity u I shall put $\dot u$, and in the same fashion for the velocities of the other quantities x, y and z, I shall write respectively $\dot x$, $\dot y$ and $\dot z$.
Having said this, I shall proceed to treating the subject introduced and I will start by giving the solution of two of the problems posed earlier.

Problem I

Given a relation between flowing quantities, determine the relation between their fluxions.

back to top

History of calculus...

Index of the guide

Next page

Home page