A Museum for Mathematics
| The Garden of Archimedes
A Museum for Mathematics |
The infinitesimal part by which a variable quantity is continually increased or decreased is called the difference of that quantity [...]The rules of differentiation for ordinary calculations are then expounded and the following sections of the volume are dedicated to the application of the calculus to geometry problems such as finding tangents, determining the maxima, minima and flexes of the curve, the study of the curvature, evolutes, caustics and envelopes.
It is evident that the difference of a constant quantity is null or zero, or (and it is the same) that constant quantities have no difference [...].
I. Request or assumption
It is required that two quantities with an infinitesimal difference can be used indifferently one instead of the other [...]
II. Request or assumption
It is required that a curve can be considered as the collection of an infinity of straight lines, each being infinitesimal, or (which is the same thing) as a polygon of an infinite number of sides, each one infinitesimal, which from the angles formed between them, determine the curvature of the line [...]
 Guillaume Francois de L'Hospital
Guillaume Francois de L'Hospital
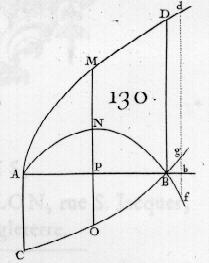
Let AMD (AP=x, PM=y, AB=a) be a curve such that the value of the ordinate y is expressed by a fraction in which the numerator and the denominator both become zero when x=a, that is when the point P falls on a given point B. The question then is, to what should the value of the ordinate BD.

 |
Johann Bernoulli
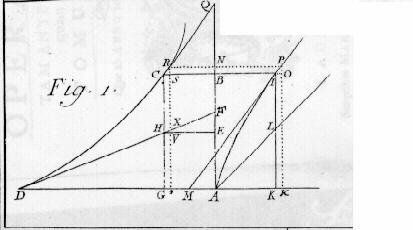
Solutio problematis Cartesio Propositi in Opera [...] The problem is therefore the following: find the curve AI such that its ordinate KI is to the subtangent KM as a given segment N is to the segment IL of the ordinate determined by the curve AI and by the line AL which forms together with the axis AK an angle equal to half a right angle. |
Up to now, geometers have used the method of maxima and minima for those problems in which among infinite parts or functions of a single given curve one looks for the maximum and the minimum; only that they have not thought of applying it there where among the infinite ungiven curves, one looks for one to which one can ascribe a certain maximum or minimum.
|
| Jacob Bernoulli
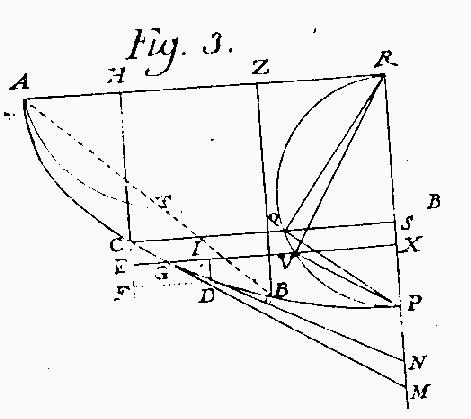
De curva celerrimi descensus In the development, we propose to the famous Nieuwentijt the use of differential-differentials (which he unjustly refuses), there where we are compelled to assume that the bit GL is even smaller than EG and GI which are already infinitely small. Without this, I do not see how the solution to the problem can emerge. EG and GI are in fact elements of the abscissa AH, just like CG, GD are elements of the curve itself, and HC, HE elements of its ordinate, and CE, EF its elements; so that having brought the problem down to pure geometry, one ends up looking for the curve the elements of which are directly proportional to the elements of the abscissa and inversely proportional to the elements of the ordinates. In truth what I observe is that this property belongs to the isochrone of Huygens, from now on also said oligochrone, commonly known to geometers as cycloid [...] |
I shall call the function of a variable quantity, a quantity that is composed in any fashion by this variable quantity and by constants.Nevertheless it is with Euler that the concept of function becomes preponderant on the less flexible concept of relation. The definition given at the beginning of the Introductio in analysin infinitorum is that of an analytical expression constructed by taking the variable
In order for this explanation to have an even wider scope, any power should be included and not only the powers of z that have positive exponents. At that point there will be no more doubt that every function z can be transformed into an infinite expression of this type:
whereThe idea of function is still distant from the modern one. The fact that the function can be described within its interval of definition by means of a single analytical expression becomes a matter of utmost importance. Only later, following various discussions regarding in particular vibrating chords, Euler will accept the possibility of there being the so called "discontinuous" functions, described by one expression within a certain interval, and by a different one in another.,
,
,
...denote any kind of number.
 |
Leonard Euler
Introductio in analysin infinitorum A constant quantity is a determinate quantity which maintains the same value. |