A Museum for Mathematics
| The Garden of Archimedes
A Museum for Mathematics |
Please note the affinity of the final passage with our
equation ![]() satisfied by the internal points of
maximum and minimum. However, while the latter is obtained making
the limit for
satisfied by the internal points of
maximum and minimum. However, while the latter is obtained making
the limit for ![]() , (iii) is obtained positing
, (iii) is obtained positing ![]() in (ii). In
the case in which
in (ii). In
the case in which ![]() is a polynomial the two procedures have the same
result, but in general it will not be possible to divide by
is a polynomial the two procedures have the same
result, but in general it will not be possible to divide by ![]() and then posit
and then posit ![]() . It is enough
to have roots in the initial equation to make the procedure
complex and inoperable. Leibniz published his Nova
Methodus, which gives birth to differential calculus,
announcing the resolution of the problem of these more complex
quantities, like irrationals. The method of maxima and minima
is used by Fermat in determining tangents, observing that the
difference between a curve and its tangent has in the tangent
point a minimum (or maximum) (see below), but this also finds
other applications. Fermat writes:
. It is enough
to have roots in the initial equation to make the procedure
complex and inoperable. Leibniz published his Nova
Methodus, which gives birth to differential calculus,
announcing the resolution of the problem of these more complex
quantities, like irrationals. The method of maxima and minima
is used by Fermat in determining tangents, observing that the
difference between a curve and its tangent has in the tangent
point a minimum (or maximum) (see below), but this also finds
other applications. Fermat writes:
The method never fails, and it can be extended to a great number of very beautiful questions: through it we have found the centre of gravity of figures limited by curved and straight lines, of solids and of many other things which I will treat separately, if we will have the time.
The first printed publication of the method is in the fifth volume of the Supplementum Cursus Mathematici (1642) written by Herigone, and only in 1679 it appears in Fermat's Varia opera mathematica as Methodus ad disquirendam maximam et minima, followed by De tangentibus linearum curvarum.
![]() Pierre de Fermat
Pierre de Fermat
De tangentibus linearum curvarum
Let us take as example the parabola BDN, with vertex D and diameter DC and point B on it, through which we must draw the straight line BE, which is tangent to the parabola and intersects the diameter in point E [...].
In order to determine the tangent to the parabola
in B, he determines, as it was customary in those times, the
subtangent, that is the segment CE. Fermat, using the maxima
and minima method, proves that CE must be equal to 2CD. To do
so, he observes that because of the properties of the parabola, ![]() , as point O is external to the
parabola. Hence, for the similitude of the triangles BCE and OIE,
we have
, as point O is external to the
parabola. Hence, for the similitude of the triangles BCE and OIE,
we have ![]() . Indicating then as D the
given quantity CD, as A the unknown quantity CE and as E the
"variation" CI, we have
. Indicating then as D the
given quantity CD, as A the unknown quantity CE and as E the
"variation" CI, we have ![]() . We now proceed as described in the general
procedure for the determination of the maxima and minima: (i)
the equation obtained "adequalising" the two terms of
the disequation, is evolved and simplified eliminating the
identical terms on the left and right; (ii) everything is divided
by E; (iii) the terms still containing E are eliminated. Thus we
arrive to the equation
. We now proceed as described in the general
procedure for the determination of the maxima and minima: (i)
the equation obtained "adequalising" the two terms of
the disequation, is evolved and simplified eliminating the
identical terms on the left and right; (ii) everything is divided
by E; (iii) the terms still containing E are eliminated. Thus we
arrive to the equation ![]() , hence
, hence ![]() , that is
, that is![]() .
.
go back
to the top of the page
The method followed by Descartes in his Géométrie to determine the tangent to a curve is more analytical-algebrical. The problem here is under the equivalent form of finding the normal to the given curve in a point. One then considers a circle with the center variable on one axis, and one imposes the algebraic condition that the circle has two intersections coinciding with the curve in the point. The method is first explained in general and then applied as an example to the ellipse and to Descartes' parabola.
 René Descartes
René Descartes
Let CE be the curve, and assume that through point C we need to draw a straight line that forms straight angles with it. I imagine everything already done and assume CP as the sought line, a line that I prolong until P where it meets straight line GA, which I imagine being that to which all the points of line CE must refer. Thus position MA or CB = y, CM or BA = x, I will obtain a certain equation that expresses the relation between x and y. [...]
With a familiar language and formalism, Descartes continues by
explaining that if one poses for the unknown circle PC=s and
PA=v, observing that the triangle PMC has a straight angle, one
has ![]() , from which one can
recover x (or equivalently, y) and substitute it in the equation
of the given curve. Then,
, from which one can
recover x (or equivalently, y) and substitute it in the equation
of the given curve. Then,
"after having found [that equation] instead of using it to know the quantities x or y [...] that are already given because point C [in which we must determine the normal to the curve] is given, we must use it to find v or s that determine the requested point P [centre of the sought circle]. For this reason, we must consider that if this point P is the way we want it, the circle of which this is the centre and that will pass through C, will touch the curve CE there without intersecting it. On the other hand, if P is a little closer or a little further from A of that which it should be, the circle will intersect the curve not only in point C but necessarily also in some other [E]. [...] but the more these two points, C and E, will be near, the less the difference between the roots [of the equation]. Finally, if these two points are one (that is if the circle that goes through C touches the curve there without intersecting it), the roots will be exactly the same [...]."
Therefore it will be sufficient to impose that
the polynomial has two double roots. If the equation of the curve
was of degree ![]() ,
the resulting polynomial will have degree
,
the resulting polynomial will have degree ![]() and will be of the form
and will be of the form ![]() where
where ![]() is a generic polynomial of
degree
is a generic polynomial of
degree ![]() . Equalising the coefficients of homologous
powers we obtain
. Equalising the coefficients of homologous
powers we obtain ![]() equations from which we can get the
equations from which we can get the
![]() coefficients of
coefficients of ![]() as well as the parameters
v and s.
as well as the parameters
v and s.
go back
to the top of the page
|
|
Franz van Schooten
In geometriam Renati Des Cartes Commentarii
|
For the specific properties of the curved line (which will be given to you), examine the various movements that the point describing the line has where you want to draw the tangent: compose all these movements in one, trace the line of the direction of the composite movement, and you will have the tangent to the curved line.
By applying the rule "word by word", one can study several curves:
tangents to conical sections, tangents to the other main curves known to the ancients and to other recently described curves, like Mr. Pascal's snail, Mr. Roberval's cycloid, Mr. Descartes's parabola of the second type, etc.
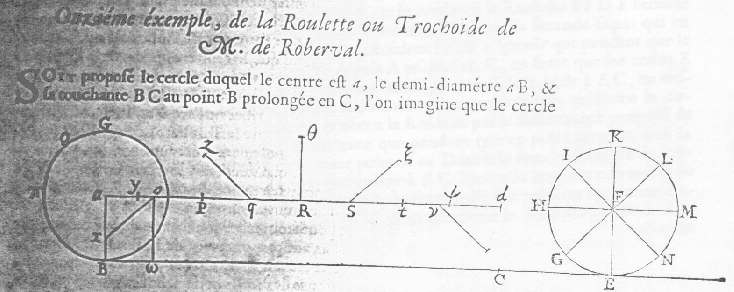 The eleventh example of
the pamphlet deals actually with the cycloid that Robertval
calls
``roulette'' o ``trochoïde''.
The
curve is described by a point B that is on a circumference as
this rolls on a straight line BC. Another way of generating
the curve is by saying that the circumference translates with
an uniform motion so that the centre
a describes the
base segment, and at the same time point B uniformly traces
the circumference. If the length of the basis is the same
than the circumference, we have a roulette of the first type,
but in general we can consider the cases in which the base is
longer or shorter than the circumference. After describing
the construction by points of the curve, Roberval describes
the construction of the tangent in any point E on the basis
of the decomposition into two simultaneous motions.
The eleventh example of
the pamphlet deals actually with the cycloid that Robertval
calls
``roulette'' o ``trochoïde''.
The
curve is described by a point B that is on a circumference as
this rolls on a straight line BC. Another way of generating
the curve is by saying that the circumference translates with
an uniform motion so that the centre
a describes the
base segment, and at the same time point B uniformly traces
the circumference. If the length of the basis is the same
than the circumference, we have a roulette of the first type,
but in general we can consider the cases in which the base is
longer or shorter than the circumference. After describing
the construction by points of the curve, Roberval describes
the construction of the tangent in any point E on the basis
of the decomposition into two simultaneous motions. Gilles Personne de Roberval
Gilles Personne de Roberval
be given; we require its tangent in point E. Describe the circle BDF of the roulette [...]; from point E draw the straight line EF parallel to AC which intersects in F the circumference of the roulette's semicircle [...]; draw FG tangent to the circle, then take H on the tangent to the circle so that AC is to the circumference of the circle like EF is to FH; from point H draw HE, and this will be the tangent to the roulette.
Roberval's construction is then compared to Fermat's:
"one draws EF as above, draws the straight line FB and through the point E draws AH parallel to FB. EH will be the tangent".
It is proven that the two construction agree, but, it is said, Fermat's method is not as general because it only works for the cycloid of the first type.
go back to the top of the page