La soluzione esatta del problema del moto rettilineo fu trovata nel 1864 da Peaucellier e, pubblicata come lettera sulla rivista Nouvelles Annales de Mathématiques, essa passò quasi inosservata. Nel 1871 Lipkin indipendentemente trovava la stessa soluzione e grandi onori gli venivano tributati dal governo russo per la presunta originalità della sua invenzione. Seppur tardivamente anche il merito di Peaucellier fu riconosciuto ed egli venne insignito di un importante premio dell'Istituto di Francia, il premio Montyon. Per completare il quadro di questa scoperta occorre ricordare che una soluzione tridimensionale era già stata descritta da Sarrus nel 1853.

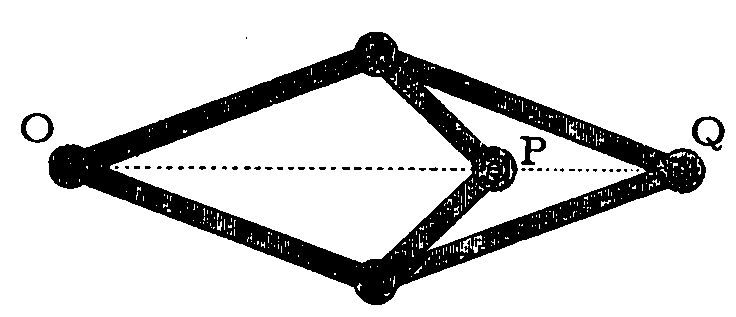
Ma veniamo a descrivere la scoperta di Peaucellier. Il suo meccanismo è costituito da sette aste incernierate. Quattro di esse della stessa lunghezza formano un rombo, due più lunghe sono incernierate a due vertici opposti del rombo e fra loro in un punto fisso O. L'apparato ora descritto è noto come cella di Peaucellier ed ha la notevole proprietà che i punti P e Q si corrispondono in una inversione circolare di centro O, cioè le distanze OP, OQ sono tali che OP · OQ = costante.

Una proprietà dell'inversione circolare, di facile dimostrazione per chi ha un minimo di pratica con la geometria euclidea, è che i cerchi passanti per il centro di inversione (nel nostro caso il punto O) vengono mandati in rette. Ciò spiega il funzionamento del meccanismo di Peaucellier: se si aggiunge una settima asta che impone a P di descrivere un cerchio passante per O allora il punto Q descriverà una retta. Una retta vera, non una sua approssimazione.

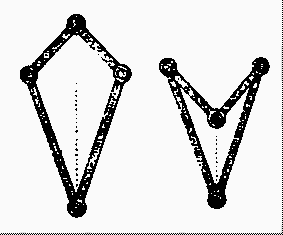
La cella di Peaucellier si può ottenere dai due quadrilateri articolati che appaiono nella figura a lato, cui la tradizione ha dato i nomi di aquilone e dardo, sovrapponendoli ed identificando le due aste più lunghe. Se la stessa operazione si esegue identificando le aste più corte otteniamo il meccanismo della figura successiva.
In questo caso si ha OQ · PQ = costante e se si costringe Q a descrivere un cerchio passante per O allora il punto P si muoverà in linea retta.

"In questa forma, che è molto compatta, il meccanismo è stato applicato con successo alle macchine usate per ventilare le Houses of Parliament [di Londra]. La scorrevolezza del funzionamento dovuta all'assenza di rumore e di frizione è veramente notevole. Le macchine furono costruite sulla base dell'apparato di Peaucellier da Mr. Prim, ingegnere della Casa del Parlamento, alla cui cortesia debbo la possibilità di averle viste: vi assicuro che esse meritano una visita", così scriveva nel 1877 il matematico inglese Kempe nel suo interessante libretto How to draw a straight line [Come tirare una linea retta]. Purtroppo tali macchine di ventilazione sono andate distrutte e non è stato possibile rintracciare alcuna documentazione.

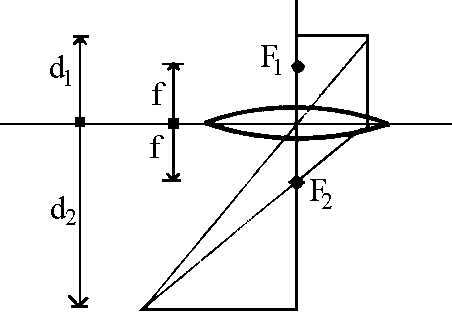
Una interessante applicazione della cella di Peaucellier si trova negli ingranditori fotografici autofocalizzanti. Se consideriamo una lente con distanza focale f, fuochi F₁, F₂, se d₁, d₂, sono le distanze dalla lente della figura da ingrandire e della figura ingrandita, si deve avere:

1/d₁ + 1/d₂ = 1/f

che equivale a:

(d₁-f) (d₂-f) = f²

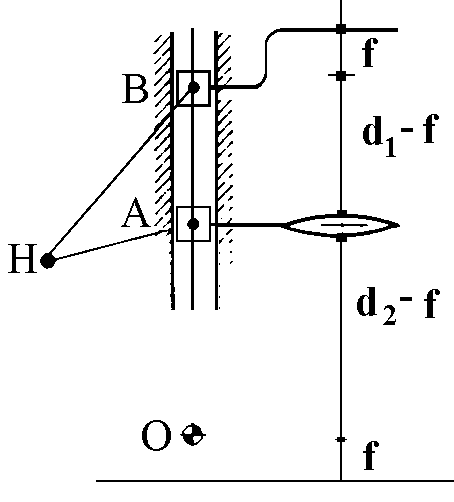
Questa equazione rappresenta una inversione fra i due segmenti di lunghezza d₁-f e d₂-f e deve essere rispettata qualunque sia l'altezza della lente, se si vuole che l'immagine proiettata sia sempre a fuoco. Si possono allora montare la lente e il portanegativo su un supporto verticale perpendicolare al piano sul quale viene proiettata la figura. L'allineamento tra i punti O, A, B è allora assicurato e quindi è sufficiente, per garantire l'inversione, una metà del meccanismo di Peaucellier composta da due aste OH e BH di lunghezza eguale incernierate nel punto comune H con un'asta AH. Il punto fisso O è posto a distanza f sopra il piano dove si forma l'immagine, mentre il punto B è reso solidale a un piano portanegativo disposto a distanza f sopra il punto B stesso. La condizione di cui sopra è verificata se si dimensionano le aste in modo che sia OH²-AH² = f².

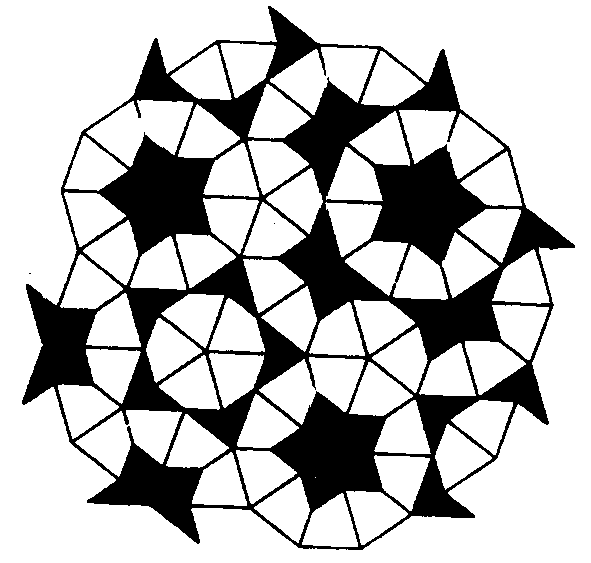
Un'ultima curiosità, quasi insignificante per noi che stiamo parlando di meccanismi ma importante in altri contesti, nel 1964 il fisico inglese Penrose trovò che per determinate lunghezze dei lati le configurazioni aquilone e dardo della figura 7 con cui è costruito il meccanismo di Peaucellier possono costituire un ricoprimento del piano non periodico, cioè che non viene trasformato in sé da nessun movimento rigido del piano.
Lo studio di questi ricoprimenti ha trovato applicazione nella teoria dei quasi-cristalli.