Il giardino di Archimede  Un museo per la matematica

Misurazioni a distanza nella Pratica della geometria di Cristofano di Gherardo di Dino

Appendice attività

• Sulle pagine introduttive
• Caso 1 (livello elementare)
• Caso 1 (livello medio)
• Caso 2
• Caso 2: il gigante (livello elementare)
• Caso 3
• Caso 4

* sulle pagine introduttive

1. Prova a dare una definizione di punto, linea, angolo, superficie, corpo.
   
2. Con l'aiuto dell'insegnante leggi le definizioni del testo e confrontale con le tue
   
3. Scrivi per ciascuno dei seguenti termini il termine corrispondente che viene usato da noi:
   
   • punto
   • linea
   • angulo
   • cantone
   • lensa
   • superfice
   • corpo
4. Identifica le ``diversità delle superfice'' descritte, fanne un disegno, scrivi il termine con cui le indichiamo e indica cosa sceglieresti come suo rappresentante

Caso 1 (livello elementare)

Misuriamo l'altezza di un albero.

• Scegli un albero e procurati un'asta. Misureremo l'altezza dell'albero in quattro modi diversi.

  
  
  

• Primo modo
  • L'asta deve essere alta quanto l'altezza dei tuoi occhi da terra.
    Misura dell'asta:........
  • Trova il punto in cui distendendoti a terra con i piedi verso l'albero e tenendo l'asta verticale tra i talloni (fatti aiutare da un compagno) vedi la cima dell'albero coincidere con la punta dell'asta.
  • Ridisegna l'albero, l'asta e la tua figura nella giusta posizione sulle linee a sinistra.
    

  • Colora di giallo il triangolo che ottieni congiungendo cima dell'albero, base dell'albero e tuoi occhi. Colora di arancione il triangolo che ottieni congiungendo cima dell'asta, base dell'asta e tuoi occhi.
  • Osserva il triangolo arancione e descrivine le caratteristiche (scaleno, isoscele, equilatero; acutangolo, rettangolo, ottusangolo). Se vi sono lati uguali segnali con una X.
  • Osserva il triangolo giallo e descrivine le caratteristiche (scaleno, isoscele, equilatero; acutangolo, rettangolo, ottusangolo). Se vi sono lati uguali segnali con //.
  • In cosa si assomigliano e in cosa differiscono i due triangoli?
  • Nel triangolo arancione ripassa con un tratto continuo i segmenti di cui conosci la misura. Nel triangolo giallo ripassa con un tratto continuo il lato che rappresenta la distanza tra i tuoi occhi e la base dell'albero e tratteggia il lato che l'altezza dell'albero.
  • Osserva la figura: il lato tratteggiato è quello che vuoi scoprire.
    

  • Misura ora ciò che ti serve e scrivi sul disegno tutte le misure che conosci.
  • Quanto sarà alto l'albero?

  
  
  

• Secondo modo
  • Prendi un'asta alta 1 metro.
    Misura dell'asta: 1 m.
  • Pianta l'asta in terra e trova il punto in cui appoggiando la testa a terra vedi la cima dell'albero coincidere con la punta dell'asta.
  • Disegna l'albero, l'asta e i tuoi occhi nella giusta posizione sul seguente schema:
    

  • Colora di giallo il triangolo che ottieni congiungendo cima dell'albero, base dell'albero e tuoi occhi. Colora di arancione il triangolo che ottieni congiungendo cima dell'asta, base dell'asta e tuoi occhi.
  • Osserva il triangolo arancione e descrivine le caratteristiche (scaleno, isoscele, equilatero; acutangolo, rettangolo, ottusangolo). Se vi sono lati uguali segnali con una X.
  • Osserva il triangolo giallo e descrivine le caratteristiche (scaleno, isoscele, equilatero; acutangolo, rettangolo, ottusangolo). Se vi sono lati uguali segnali con //.
  • In cosa si assomigliano e in cosa differiscono i due triangoli?
  • Ripassa a tratto continuo i segmenti di cui conosci la misura o che puoi misurare facilmente; ripassa a tratteggio l'altezza dell'albero che non puoi misurare direttamente e che vuoi scoprire.
  • Scrivi sul disegno le misure che conosci, dopo aver compiuto le misurazioni necessarie.
  • Per scoprire quanto sarà l'altezza dell'albero, osserva cosa succede nei triangoli rappresentati sotto. Ripassa a tratteggio e a tratto continuo i cateti dei due triangoli come nella situazione reale; usando l'unità di misura indicata (che rappresenta l'asta di 1 metro), scrivi le tre misure dei lati a tratto continuo. Fai poi una previsione sul lato che rappresenta l'altezza della torre. Verifica la tua previsione misurando tale lato e scrivi la misura sul disegno.
    

  • Torna ad osservare la figura e le tue misurazioni. Quanto sarà alto l'albero?
  • Quali operazioni hai compiuto per calcolare la soluzione?

  
  
  

• Terzo modo
  • Prendi un'asta di altezza qualsiasi.
    Misura dell'asta: ..........
  • Pianta l'asta in terra e trova il punto in cui appoggiando la testa a terra vedi la cima dell'albero coincidere con la punta dell'asta.
  • Disegna l'albero, l'asta e i tuoi occhi nella giusta posizione sul seguente schema:
    

  • Colora di giallo il triangolo che ottieni congiungendo cima dell'albero, base dell'albero e tuoi occhi. Colora di arancione il triangolo che ottieni congiungendo cima dell'asta, base dell'asta e tuoi occhi.
  • Osserva il triangolo arancione e descrivine le caratteristiche (scaleno, isoscele, equilatero; acutangolo, rettangolo, ottusangolo). Se vi sono lati uguali segnali con una X.
  • Osserva il triangolo giallo e descrivine le caratteristiche (scaleno, isoscele, equilatero; acutangolo, rettangolo, ottusangolo). Se vi sono lati uguali segnali con //.
  • In cosa si assomigliano e in cosa differiscono i due triangoli?
  • Ripassa a tratto continuo i segmenti di cui conosci la misura o che puoi misurare facilmente; ripassa a tratteggio l'altezza dell'albero che non puoi misurare direttamente e che vuoi scoprire.
  • Scrivi sul disegno le misure che conosci, dopo aver compiuto le misurazioni necessarie.
    

  • Per scoprire quanto sarà l'altezza dell'albero, osserva cosa succede nei seguenti triangoli. Ripassa a tratteggio e a tratto continuo i cateti dei due triangoli come nella situazione reale. Usando l'unità di misura indicata (che rappresenta 1 metro), scrivi le misure dei cateti del triangolo arancione e del triangolo giallo.
    

  • Osserva le misure che hai ottenuto per ciascun triangolo. Cosa scopri?
  • In ciascuna coppia di triangoli potresti allora dire quanto misura il lato tratteggiato misurando solo gli altri tre cateti? Come?
  • Torna ad osservare la figura e le tue misurazioni. Quale sarà allora la misura del cateto tratteggiato?
  • Hai scoperto la misura dell'albero!

  
  
  

• Quarto modo
  • Prendi un'asta più alta di quanto i tuoi occhi siano alti rispetto al suolo.
    Misura dell'altezza dei tuoi occhi dal suolo: .........
    Misura dell'asta: ...........
  • Pianta l'asta in terra e arretra fino al punto in cui vedi la cima dell'albero coincidere con la punta dell'asta.
  • Disegna l'albero, l'asta e i tuoi occhi nella giusta posizione sul seguente schema:
    

  • Colora di giallo il triangolo che ottieni congiungendo la cima dell'albero, il punto dell'albero all'altezza dei tuoi occhi e i tuoi occhi. Colora di arancione il triangolo che ottieni congiungendo la cima dell'asta, il punto dell'asta all'altezza dei tuoi occhi e i tuoi occhi. Colora di viola il rettangolo che rimane.
  • Osserva il triangolo arancione e descrivine le caratteristiche (scaleno, isoscele, equilatero; acutangolo, rettangolo, ottusangolo). Se vi sono lati uguali segnali con una X.
  • Osserva il triangolo giallo e descrivine le caratteristiche (scaleno, isoscele, equilatero; acutangolo, rettangolo, ottusangolo). Se vi sono lati uguali segnali con //.
  • In cosa si assomigliano e in cosa differiscono i due triangoli?
  • Ripassa a tratto continuo i segmenti di cui conosci la misura o che puoi misurare facilmente; ripassa a tratteggio l'altezza dell'albero che non puoi misurare direttamente e che vuoi scoprire.
  • Scrivi sul disegno le misure che conosci, dopo aver compiuto le misurazioni necessarie.
    

  • Facendo finta che il rettangolo viola non ci sia sei nella stessa situazione precedente. Come puoi allora calcolare l'altezza dell'albero?
    Per il pezzo tratteggiato: ..........
    Per tutto l'albero: ..........
• Quale dei modi suggeriti per scoprire l'altezza dell'albero ti sembra migliore? Perché?
• Leggiamo il passo in cui Cristofano spiega come misurare l'altezza di una torre:

  Se vuoi sapere l'altessa d'alcuna torre, pone una asta ricta in del piano dinanti a te di ver la torre, et sia più lungha che tu si' come vedi in questa prezente fighura; et sia l'asta 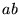$ab$ et tu sia 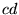$cd$. Et or righuarda movendoti, là e qua in dietro e innansi, sicchè tu veggi per lo 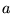$a$ la sommità della torre, cioè lo punto $f$.

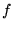• Quale dei quattro modi è quello suggerito da Cristofano?
• Riscrivi la sua spegazione usando un linguaggio più moderno e prova anche a scrivere come si deve procedere per calcolare la soluzione.

Caso 1 (livello medio)

• Leggi la descrizione di Cristofano. Riscrivi il passo secondo la spiegazione che daresti tu oggi.
• Fai un disegno schematico della situazione.
• Quali misure ti occorrono per conoscere l'altezza 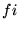$fi$? Quali dipendono dall'oggetto da misurare e quali dall'osservatore e dallo strumento che usa?
• Come risolveresti il problema? ¹³
• Confronta il tuo procedimento risolutivo con quello di Cristofano e scrivi le tue osservazioni su analogie e differenze.
• Prova ora a misurare l'altezza di una torre o più semplicemente di una casa, un palazzo o di una finestra di un palazzo, di un palo o di una qualsiasi altra cosa a tua scelta usando la tecnica precedente.
  Descrivi il procedimento che segui per la misurazione e per il calcolo. ¹⁴

Caso 2

• Leggi il passo di Cristofano.
• Riscrivi le procedure di misurazione facendo anche un disegno schematico.
• Applica il procedimento ad una situazione reale o immaginaria:
  • Individua le misure di cui hai bisogno.

    Avrai bisogno delle seguenti misure:

    • la tua altezza $cd=mn=...$
    • l'altezza dei bastoni che utilizzi $ab=kl=...$
    • la tua distanza dal bastone nella prima posizione $cg=...$
    • la tua distanza dal bastone nella seconda posizione $em=...$
    • la distanza tra la tua prima posizione e la tua seconda posizione $cm=...$

  • Calcola l'altezza cercata illustrando il procedimento matematico.

Caso 2 ter: il gigante (livello elementare)¹⁵

• Un gigante ha rinchiuso la principessa sulla cima di una torre circondata da un fossato. Tu, cavaliere in cerca di avventure, devi liberarla. Come fare? Il ponte levatoio si può azionare facendo infilare dall'alto in un meccanismo alla base della torre una grossa chiave che la principessa ha. Le dirai allora di tagliare il suo mantello e annodandolo realizzare una fune a cui annodare la chiave che arrivi esattamente fino alla base della torre. Ma per fare ciò devi saperle dire quanto è alta la torre. Hai a disposizione qualche bastone raccolto nella foresta.
• Preparativi: scegli un bastone come riferimento che farà da unità di musura (ad esempio lungo ``un gomito''; potresti sceglierlo lungo un metro, ma è improbabile che la principessa sulla torre possa poi misurare la fune in metri, mentre sicuramente ha a disposizione il suo braccio per effettuare la misura) e ne realizzi varie copie con cui misurerai le distanze necessarie; costruisci poi due aste che conficcate nel terreno siano esattamente un gomito più alte di te.
  fig. 2
• Pianta la prima asta in un punto 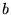$b$ e arretra fino a vedere la principessa allineata con la cima dell'asta. Misura con i bastoni la tua distanza dall'asta.
  Ricorda che se disti ad esempio 5 bastoni dall'asta sai anche che disti 5 volte l'altezza della torre dalla torre stessa.
  fig. 3: taglia i bastoni necessari dalla fig. 2 e incollali sul tratto $cg$; ritaglia anche lo stesso numero di unità-torre e incollale sul tratto $ch$.
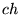• Ripeti la stessa procedura piantando l'asta nel punto 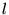$l$. Misura quanti bastoni disti dall'asta; questo è anche la tua distanza dalla torre misurata in unità-torri. fig. 4: taglia e incolla bastoni e torri come sopra.
• Conta ora quanti bastoni e quante torri misurano il tratto $cm$. Se ad esempio avrai 2 torri e 24 bastoni avrai scoperto che la torre è alta 12 bastoni: la principessa è salva.

Caso 3

• Leggi il passo di Cristofano.
• Esegui un disegno schematico della situazione.
• Descrivi lo strumento utilizzato.
• Applica il procedimento a una situazione reale o immaginaria e descrivi la soluzione seguendo lo schema
  • Oggetto prescelto: .......
  • Misurazioni da effettuare
    • $ef$
    • $eh$
    • $fh$
  • Si hanno le seguenti proporzioni:
    • $fe:1=...:...$

    • $he:2=...:...$

  • Allora
    • $fg=fe \cdot ga$
    • $hg=...$

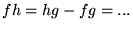  • Dunque $fh=hg-fg=...$ e sostituendo i valori noti ...
  • e quindi $ga=...$.
    

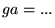  • Infine essendo la mia altezza ... ottengo che l'altezza dell'oggetto scelto è $...+...=$

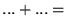
Caso 4

Dopo aver letto il passo di Cristofano applica lo stesso procedimento per misurare l'altezza di un oggetto.

• Oggetto prescelto: ..........
• Misure di cui hai bisogno:
  • la tua altezza ($dc=dk=...$)
  • la tua distanza dallo specchio nella prima posizione ($bc=...$)
  • la tua distanza dallo specchio nella seconda posizione ($tk=...$)
  • la distanza tra la prima e la seconda posizione dello specchio ($bt=...$)

• Triangoli simili da utilizzare:
  • ... e ...
  • ... e ...

• Proporzioni
  • $bc:cd=be:...$
  • $tk:kd=...:...$

• Sostituendo i valori noti $... \cdot ea = ...$, da cui $ea=...$.

Misurazioni a distanza nella Pratica della geometria di Cristofano di Gherardo di Dino

Il Giardino di Archimede per la Storia della matematica a scuola

Pagina principale de Il Giardino di Archimede