Il giardino di Archimede  Un museo per la matematica

Pitagora e il suo teorema

I solidi regolari

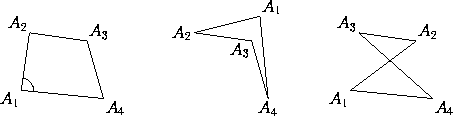
	Tra le scoperte attribuite a Pitagora c'è quella delle figure cosmiche, ossia dei solidi regolari. Per capire di che si tratta dobbiamo prima dire due parole sui poligoni. Un poligono è una figura piana delimitata da una spezzata, i cui segmenti sono i lati del poligono. I punti in cui due lati si toccano si chiamano vertici del poligono; gli angoli che i lati formano a ogni vertice sono gli angoli del poligono. Ogni poligono ha tanti lati quanti vertici e angoli; esso prende il nome da questo numero. Ad esempio un poligono con tre angoli (dunque con tre lati e tre vertici) si chiama triangolo, quello con quattro quadrilatero, con cinque pentagono (dal greco pente, cinque e gonia, angolo) e poi di seguito esagono, ettagono, eccetera. Lo stesso nome poligono viene da polys, molti, e gonia. Si noterà la differenza tra triangolo, quadrilatero, e gli altri poligoni.
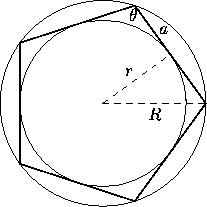
	Un poligono si dice regolare se ha tutti i lati e tutti gli angoli uguali. Per costruirne uno, si può dividere una circonferenza nel numero desiderato di parti, e unire i punti di divisione. Così un pentagono regolare si ottiene dividendo la circonferenza in cinque parti uguali, come in figura. Una proprietà dei poligoni regolari di cui ci serviremo è che i loro angoli aumentano all'aumentare del numero dei lati; gli angoli di un triangolo equilatero sono di 60 gradi, quelli di un quadrato di 90 gradi, il pentagono regolare ha angoli di 108 gradi, l'esagono regolare di 120 gradi, eccetera.
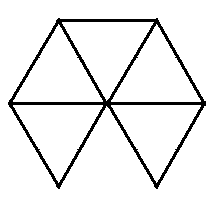
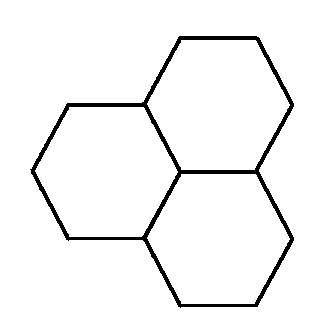
	Passiamo ora ai poliedri o solidi regolari, solidi le cui facce sono dei poligoni regolari tutti uguali tra loro, e tali che in ogni vertice confluiscono lo stesso numero di facce. Le facce si attaccano lungo gli spigoli, i quali a loro volta confluiscono nei vertici, punti attorno ai quali sono situate tre o più facce. A differenza dei poligoni regolari, che possono avere un qualsiasi numero di lati, ci sono solo cinque solidi regolari: tre con facce triangolari, uno con facce quadrate e uno con facce pentagonali. Per capire il motivo di questo comportamento, prendiamo un solido regolare, e guardiamo cosa succede intorno a un suo vertice, lasciando solo le facce che stanno attorno a questo vertice, e tagliando via tutte le altre. Se ora facciamo ancora un taglio lungo uno spigolo, la superficie che resta si può stendere su un piano. Quello che vediamo è un certo numero (tre o più ) di poligoni regolari uguali, che si toccano tutti nel vertice, più un certo angolo che si produce quando si apre il poliedro per distenderlo sul piano. La somma degli angoli che stanno attorno al vertice è dunque minore di 360 gradi, e siccome attorno al vertice ci sono almeno tre poligoni, questi devono avere angoli minori di un terzo di 360 gradi, cioè minori di 120 gradi. Ma come abbiamo visto ci sono solo tre poligoni regolari con angoli minori di 120 gradi: il triangolo, il quadrato e il pentagono. Già l'esagono ha angoli di 120 gradi, e dunque tre esagoni riempiono tutto lo spazio attorno al vertice e non lasciano nessun angolo per richiudere il poliedro.
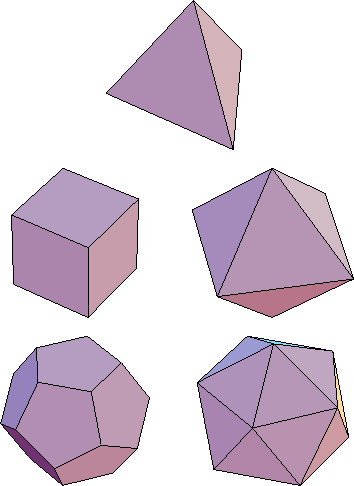
	Sono dunque possibili solo solidi regolari con facce di tre, quattro o cinque lati. Nei due ultimi casi intorno a un vertice ci possono essere solo tre facce (quattro quadrati riempiono tutto lo spazio attorno al vertice, quattro pentagoni fanno più di 360 gradi); i solidi rispettivi sono il cubo e il dodecaedro, il primo con sei facce quadrate, il secondo con dodici facce pentagonali. Nel caso di facce triangolari, ognuna delle quali ha un angolo di 60 gradi, attorno a un vertice ci possono essere tre, quattro o cinque facce, ma non sei, che riempirebbero tutto lo spazio disponibile. I solidi corrispondenti sono il tetraedro che ha in totale quattro facce, l'ottaedro con otto, e l'icosaedro con venti.