| |
|
|
 |
The simplest mechanism of hinged axes is the articulated quadrilateral.
Let's consider the quadrilateral ABCD with the fixed side AD. It's clear that
the position of one of the three axes determines the positions of the remaining
ones. This is a mechanism with only one degree of freedom.
|
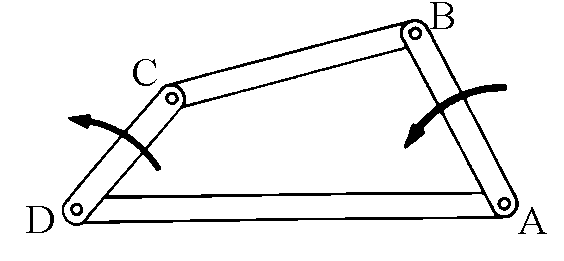 |
If we rotate the axis CD anticlockwise, the axis AB will also be rotated anti-clockwise.
By varying the relation between the lengths of the axes,
the articulated system changes. Our exhibit shows how one can
describe curves with very different shapes by using this very simple mechanism.
|
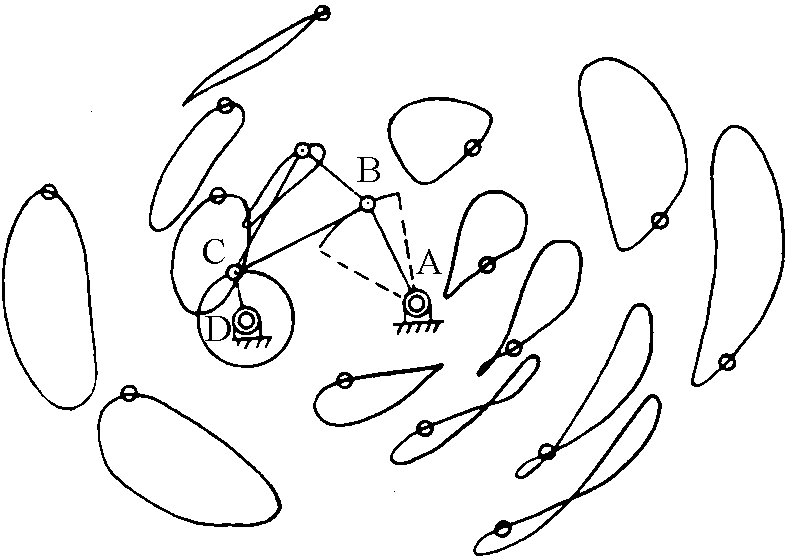 |
The articulated quadrilateral is determined by the points ABCD, of which A and D are fixed.
By moving the shorter axis (CD), the change in position
of the remaining axes AB and CB is determined.
Considering a plane integral with the
axis CB (the plane of the plexiglas of the exhibit),
the points of such a plane will describe curves of different shapes,
depending on the position of the point.
To isolate the tracing point of the plane fixed to the axis BC, it is
sufficient to add to the mechanism two more axes BE and CE which form a triangle with BC.
|
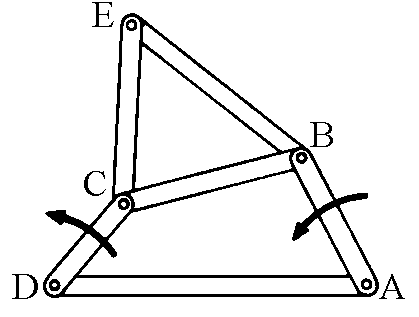 |
The curves described by the point E, depending on its position on the
plane integral to the axis CB, have very different shapes. Some are ovoidal,
some are almost rectilinear and others are shaped like an elongated eight.
Numerous applications of the articulated quadrilateral can been
seen in things we use every day;
a balance (scales) , venetian blinds, some table lamps
, hoists , the pedals
of old sewing machines.
These are some of the objects in which the articulated quadrilateral is used.
The type of articulated quadrilateral in question is one
with opposing, parallel axes of equal length.
|
|
|