The Garden of Archimedes  A Museum for Mathematics

Integration and measure

|    integration and measure    |   
|    from Cauchy    |    from Riemann    |    from Peano    |    from Jordan    |    from Lebesgue    |

The same rigorous criteria that Cauchy had adopted in the Cours d'analyse are followed in presenting the fundamental concepts of calculus in the second of treaties he wrote for students of his courses, the Résumé des leçons données à l'École Royale Polytechnique. The last lectures of the course (XXI to XL) are devoted to integration.

"In integral calculus" - he writes in the introduction - "I thought it necessary to demonstrate in general the existence of the integrals or primitive functions, before revealing their various properties. For that, it was first of all necessary to establish the notion of an integral taken between two given limits, or defined integral."

The integral is thus defined independently from the derivate, but then the two operations are compared, with a point of view in a way more similar to the ideas on the measure of figures that had developed with Cavalieri and his followers, and that had been swept apart with the success of infinitesimal calculus, when the aspect of integration as the inverse operation than differentiation prevails.
In order to define the integral of a function $f(x)$ continuous with $x$ varying in the interval $[x_o, X]$ he considers a partition $P$ of the interval in the elements $x_1-x_o$, $x_2-x_1$, ..., $X-x_{n-1}$, and defines the sum relative to $P$, nowaday called "Cauchy's", as $S= (x_1-x_o)f(x_o)+ (x_2-x_1)f(x_1)+ ...+ (X-x_{n-1})f(x_{n-1})$. Having established that, he proves that, thickening the partition, the intervals become "very small",

the value of $S$ will end up being visibly constant, or in other words will end up reaching a certain limit that will only depend on the form of the function $f(x)$ and on the extreme values attributed to variable $x$. This limit is what is called a defined integral.

Cauchy's new idea still presents many incomplete or unsatisfactory aspects, on which later discussions develop. For example, the lack of a clear distinction between continuity and uniform continuity, which was later the object of studies by Weierstrass and his school; the lack of a systematisation of irrational numbers that makes the existence of a limit of sums ambiguous.
A particularly serious shortcoming, especially in the treatment of Fourier series, is that the definition is valid for continuous functions or functions with a finite number of discontinuities.
In the last part of his 1829 memo on Fourier series, Sur la convergence des séries trigonométriques, Dirichlet raises the issue of the integrability of functions with an infinite number of discontinuity points, claiming that the set of admissible discontinuities must be such that, translated into modern terms, its closure has no internal points. As evidence of his claim, he brings the famous example of the function bearing his name, that is the function $f(x)$ whose value is 1 if $x$ is rational and 0 if is $x$ not rational, claiming that it is a non-integrable function.
A new definition of integral that extends the class of integrable functions to functions with an infinite number of discontinuity points is given by Bernhard Riemann in his tenure habilitation thesis titled Ueber die Darstellbarkeit einer Funktion durch eine trigonometrische Reihe, which is dated 1854 but remains practically unknown until 1867, when Dedekind publishes it.
Here Riemann introduces the integral that bears his name, considering the sums approximating from above and from below. He then considers the problem of characterising integrable functions. The final results are basically the following:

The necessary and sufficient condition to the integrability of a limited function $f(x)$ is that for every $\sigma>0$ and $\delta>0$ there exists a partition of the definition interval into a finite number of intervals, such that the sum of the lengths of those in which the oscillation of the function is above $\sigma$ is smaller than $\delta$.

The general nature of this condition is shown by constructing an example of integrable function which satisfies it, and which has a dense set of discontinuity points, in contrast with the condition that Dirichlet considered necessary.
The publication of Riemann's memo spurred a series of studies which brought about developments in various directions. On the one hand, a specification of topological concepts and of the properties of the straight line, which lead Cantor to the foundation of set theory, and on the other, the construction of a theory of measure which led to Lebesgue's theory.
In the years that followed, a number of works appeared, dealing with the study of the discontinuity set of integrable functions that involve the jumps or oscillations of the function, sparse sets, negligible sets, sets of the first species (that is, with an empty nth derivate); among which we find contributions by Hankel, Vitali, Du Bois-Reymond, Smith, Volterra. An organic systemisation of these first developments on Riemann's integral can be found in the Foundations for a theory of real variable functions (1878).
Beside the topological characterisations, the idea of a "measure" of sets slowly develops. Stolz and Harnack for example define the "content" ("Inhalt") of a set as the lower bound of the sum of the lengths of the intervals whose union excludes the given set. Cantor, at the same time, considers it the lower bound of the measures of the external envelopes.
A more articulate concept of content is introduced by Peano in 1887's Geometric Applications of Integral Calculus. Jordan, in the second edition of the Cours d'Analyse, develops a similar but more general tractation of n-dimensional space, with the use of pluri-intervals. One defines the outer measure of a set A as the lower bound of the measures of the pluri-intervals that contain A, and as inner measure of A the upper bound of the measures of the pluri-intervals contained in A. A set will then be measurable (according to Peano and Jordan) if its inner and outer measures coincide.
Peano-Jordan's measure, thus defined, results as additive (that is the measure of the union of two measurable disjointed sets coincides with the sum of their measures) but not numerably additive.
Harnack had already raised the issue of whether the sum of the measures of a numerable infinity of disjointed intervals whose union is the interval (a, b) were equal to b-a, believing he could answer negatively.
The issue was taken up again from a different point of view by Borel, who demonstrated the result that Harnack had believed false and uses it as a starting point for an axiomatic definition of measure, nucleating the properties that he considered essential:

a)

the measure of an interval (open or close) is given by the difference between its extremes

b)

the measure of the difference between two measurable sets A and B with $A \supset B$, is the difference between the measures

c)

the measure of the union of a numerable infinity of measurable disjointed sets is the sum of the measures.

Borel then indicates how to construct a class of sets, which were later called "Borel sets", which are measurable in this sense. These are the minimum class containing the intervals which is stable according to difference and to measurable union.
Borel's theory represents a great step forward, especially because of the numerable additivity which was to reveal itself as one of the most productive properties. In Borel's work, it appears, however, as a technical means for the study of other issues, and is treated in an incomplete and almost marginal way.
Lebesgue first understood the importance of the new ideas and reworked them in his theory, which finds a first complete exposition in the thesis Intégrale, longueur, aire published in 1902 on the "Annals of Mathematics", and which is posed in a definitive way in the Leçons sur l'intégration et la recherche des fonctions primitives published in 1904.
Regarding measure, he joins Borel's ideas with Peano's and Jordan's, defining firstly the external measure of a set E as the lower extreme of the measures of the open sets that contain E; then, in the case that E is limited and therefore contained in an interval Q, he defines the outer measure of E as the difference between the measure of Q and the outer one of Q-E. A set will be measurable if its inner and outer measures coincide. Lebesgue then demonstrated that the difference of two measurable sets is measurable and that the union of a numerable infinity of measurable sets is measurable, and therefore finds again Borel's conditions b) and c).
Lebesgue's most important contribution is, however, the application of these ideas to integration theory. Lebesgue himself muses on the difference between his definition of integral and Riemann's, in his popular Sur le development de la notion d'intégrale, also using the comparison between the way a disorganised merchant counts coins, and the way another will order them according to size. In essence, having a much more flexible measurement available allows one to have approximations which are no longer construed through a partition into sub-intervals of the definition interval of the function to integrate, but through a partition of the definition set into more general subsets on the basis of the values which the function assumes.
Measure is not used any more to characterise the discontinuity of functions that were integrable according to Riemann, but to enlarge the class of functions that can be integrated. Moreover, the use of a numerably additive measure, as well as making a great number of sets measurable, brings about similar properties for the integral. This then can enjoy more efficient properties such as that of passage to the limit under the sign of integral, one of the cornerstones of the theory and a very powerful instrument in many applications.

go back to the top of the page

The definition of integral in Cauchy's Résumé des leçons données à l'école Royale Polytechnique

* Page IX.1 in the exhibition

Luis Augustin Cauchy
Résumé des leçons données à l'école Royale Polytechnique

Let us suppose that, $f(x)$ being a continuous function on the variable $x$ between two finite limits $x=x_o$ and $x=X$, one denotes as $x_1$ , $x_2$ , ..., $x_{n-1}$ some new values of $x$ interposed between those limits, and that always increase or decrease from the first limit to the second. One can use these values to divide the difference $X-x_o$ into the elements $x_1-x_o$, $x_2-x_1$, $x_3-x_2$, ... $X-x_{n-1}$, which will all have the same sign. Having posited that, let us imagine that we multiply each element by the value of $f(x)$ corresponding to the origin of the same element, that is the element $x_1-x_o$ by $f(x_o)$, the element $x_2-x_1$ by $f(x_1)$, and finally the element $X-x_{n-1}$ by $f(x_{n-1})$; let $S= (x_1-x_o)f(x_o)+ (x_2-x_1)f(x_1)+ ...+ (X-x_{n-1})f(x_{n-1})$ be the sum of products thus obtained. Quantity S will obviously depend: 1)on the number n of the elements into which the difference $X-x_o$ will be divided; 2) on the values of these elements themselves, and, consequently, on the subdivision method adopted. Now it is important to remark that if the numerical values of elements become very small and the number n very big, the subdivision method will have an invisible influence on the value $S$[...]

go back to the top of the page

The definition of integral in Riemann's Über die Darstellbarkeit einer Funktion durch eine trigonometrische Reihe

* Page IX.2 of the exhibition

Bernhard Riemann
Über die Darstellbarkeit einer Funktion durch eine trigonometrische Reihe

The incertitude that reigns on some fundamental points of the theory of undefined integrals forces us to preface with some words on the concept of defined integral and on the scope of its validity. Then, first of all: what is meant by $\int ^a_b f(x) \,dx$? To establish that, let us take between a and b a series of values $x_1$, $x_2$, ..., $x_{n-1}$ that follow each other, and let us denote for brevity $x_1-a$ as $\delta_1$ , $x_2-a$as $\delta_2$ ,..., $b-x_{n-1}$ as $\delta_n$ and as $\varepsilon$ a proper positive fraction. The value of the sum

$$S= \delta_1 f(a+ \varepsilon_1\delta_1)+ \delta_2 f(a+ \varep... ...varepsilon_3\delta_3)+...+ \delta_n f(a+ \varepsilon_n\delta_n)$$

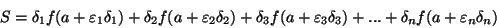
will then depend on the choice of intervals $\delta$ and of $\varepsilon$. If it has the property, no matter how chosen $\delta$ and $\varepsilon$, of infinitely approximating a prefixed limit A, as soon as they will become infinitely small, then this value is called $\int ^a_b f(x) \,dx$ [...]

go back to the top of the page

Measure in Peano

* Page IX.3 of the exhibition

Giuseppe Peano
Applicazioni geometriche del calcolo integrale

The points of a straight line that are between two given points, considering or not considering those two points, form a field, which is called a rectilinear segment. Its length is a principal quantity: every field formed by a finite number of segments also has a length comparable to that of a given segment.
Let us take now a field formed by points on a straight line, no matter how given. We can, in general, imagine fields made of a finite number of segments, of which the given field is part, and we could imagine other fields also made of a finite number of segments, which are part of the given field. Each of these fields has a length, and the length of the former is greater than the length of the latter.
If the lower limit of the length of the first fields coincides with the upper limit of the lengths of the seconds, to this common value we will give the name of length of the given rectilinear field. But it could be that those limits are not equal, and therefore that the lower limit of the former lengths is greater than the upper limit of the latter. In this case we will say that the proposed field does not have a length comparable to that of a rectilinear segment, and to the lower limit of the former lengths we can give the name of external length of the given field, and call its internal length the upper limit of the latter.

go back to the top of the page

Measure in Jordan.

* Page IX.4 of the exhibition

Camille Jordan
Cours d'analyse de L'école Polytechnique

36. We will then try to narrow the concept of extension of this object (which we can call in particular length, area, or volume, when the number of dimensions is 1, 2 or 3).
To fix down ideas, let us consider the case of two dimensions. Each point (u,v) of E can be geometrically represented on a plane of which u and v are the coordinates. Let us decompose this plane, with parallels to the axes, into squares with sides r. Among these, the set of the squares that are internal to E form a domain S internal to E; the set of those which are internal to E and that intersect its boundary form a new domain S+S' to which E is internal. These domains have a determined area that we will indicate, again, as S and S+S'.
Let us vary our decomposition into squares so that r tends to zero; areas S and S+S' will tend towards fixed limits [...].

go back to the top of the page

Borel's measure.

* Page IX.5 of the exhibition

Émile Borel
Leçons sur la théorie des fonctions

Here are the new definitions: if a set E has as a measure s, and contains all the points of a set E' the measure of which is s', we can say that set E-E', formed by the points of E that do not belong to E', has the measure s-s'; moreover, if a set is the sum of a numerable infinity of sets with no parts in common, its measure will be the sum of the measures of its parts, and finally if the sets E and E' have, because of these definitions, measures s and s' and E includes all the points of E', the set E-E' will have the measure s-s'.
The fundamental theorem which we have demonstrated on page 41-43 assures us that these definitions will never be in contradiction with each other; we are therefore free to adopt them; we are also confident that the measure of a set can never be a negative quantity; but a set can have a measure zero and the power of the continuum. Thus is the set E considered below [...].

go back to the top of the page

The measure of Lebesgue.

* Page IX.6 of the exhibition

Henri Lebesgue
Intégrale, longueur, aire

3. Given a set $E$ one can in an infinite variety of ways include its points in an interval or in a numerable infinity of intervals. The set $E_1$ of the points of these intervals contains $E$, therefore measure $m(E)$ of $E$ is at most equal to the one $m(E_1)$ of $E_1$, that is at most equal to the sum of the lengths of the intervals considered. The lower limit of this sum is an upper limit of $m(E)$; we will call it the outer measure of $E$, $m_e(E)$.
Let us suppose that all the points of $E$ belong to a segment $AB$. We will call a complementary of $E$ by $AB$, $C_{AB}(E)$, the set $AB-E$. Since the measure of $C_{AB}(E)$ is at most $m_e[C_{AB}(E)]$, the measure of $E$ is at least $m(AB)- m_e[C_{AB}(E)]$. This number does not depend on the segments containing $E$ chosen; we will call it the inner measure of $E$, $m_i(E)$[...].

We will call a measurable set that whose inner and outer measures are equal, the common value of these two numbers will be the measure of the set, if the issue of measure is possible. From the properties that follow it will result that the number $m(E)$ thus defined satisfies the conditions of the measurement problem if one only considers the measurable sets.

go back to the top of the page

History of calculus

Index of the guide

Main page