Un museo per la matematica
| Il giardino di Archimede
Un museo per la matematica |
La geometria delle curve:
|
| |
Le prime linee che si presentano all'immaginazione dell'uomo sono la retta e il cerchio. Con esse nasce la geometria, il cui nome, letteralmente misura della terra, indica chiaramente a quale fine esse fossero dirette. I primi geometri dell'antichità sono gli agrimensori dell'antico Egitto. I greci danno loro il nome di arpedonapti, annodatori di corde. Tirando le funi, i geometri egizi potevano tracciare sul terreno rette e cerchi, un'operazione di cui resta una traccia in molte lingue moderne, nell'espressione "tirare una retta". L'uso delle corde per operazioni sul terreno permane inalterato per molti secoli, e si ritrova nel lavoro degli agrimensori anche in tempi relativamente recenti.
Le testimonianze degli storici greci vogliono che la geometria (letteralmente: misura della terra) sia nata in Egitto. Dice Erodoto:
Se poi il fiume aveva semplicemente cancellato i confini dei campi, era compito degli stessi funzionari ristabilire le giuste divisioni.
 Gli agrimensori egizi erano chiamati "arpedonapti", annodatori di funi. E tirando le funi essi tracciarono le due linee più semplici e più importanti della geometria: la retta e il cerchio. La prima, semplicemente tendendo una fune tra due punti, un'operazione di cui resta ancora un'immagine nelle espressioni "tirare una retta", "tirare una perpendicolare"; il secondo, facendo ruotare uno di questi attorno all'altro che rimane fisso. Immaginavano a quale ricchezza di costruzioni potessero condurre queste due pratiche così elementari? Probabilmente no. Di certo però la necessità di costruzioni del tipo di quelle che oggi chiamiamo "con riga e compasso", ma che più propriamente forse si dovrebbero dire "con cerchi e rette", dovette emergere subito dalle esigenze pratiche del lavoro degli agrimensori.
Gli agrimensori egizi erano chiamati "arpedonapti", annodatori di funi. E tirando le funi essi tracciarono le due linee più semplici e più importanti della geometria: la retta e il cerchio. La prima, semplicemente tendendo una fune tra due punti, un'operazione di cui resta ancora un'immagine nelle espressioni "tirare una retta", "tirare una perpendicolare"; il secondo, facendo ruotare uno di questi attorno all'altro che rimane fisso. Immaginavano a quale ricchezza di costruzioni potessero condurre queste due pratiche così elementari? Probabilmente no. Di certo però la necessità di costruzioni del tipo di quelle che oggi chiamiamo "con riga e compasso", ma che più propriamente forse si dovrebbero dire "con cerchi e rette", dovette emergere subito dalle esigenze pratiche del lavoro degli agrimensori.
Oggi è così naturale considerare il foglio come il terreno naturale della geometria, che percepiamo l'uso esclusivo della riga e del compasso come una limitazione arbitraria, introdotta da spiriti speculativi che preferivano la ristrettezza del numero degli assiomi alle comodità derivanti dalla molteplicità degli strumenti; cosicché il geometra teorico -parlo qui naturalmente del geometra classico, euclideo- si distingue dal tecnico -agrimensore, architetto- soprattutto perché il primo si preclude volontariamente l'uso di strumenti, squadre, pantografi, che invece il secondo utilizza con profitto.
Così facendo, trascuriamo totalmente la geometria "in campo" a favore di quella "in carta", e non vediamo che per essere trasportate sul terreno, le operazioni geometriche hanno bisogno di tecniche e accorgimenti diversi, talora totalmente, da quelle che avevano la preminenza nella scala ristretta del foglio.
Senza contare poi che la precisione del disegno è molto più necessaria sul terreno (all'agrimensore che divide e misura i campi, come all'architetto, spesso la stessa persona, che erige edifici) di quanto non sia sulla carta. All'architetto che ha chiaro il progetto generale e ricorda i propositi che lo hanno guidato nella progettazione, può ben bastare un disegno di massima; le mappe catastali, non solo quelle dell'antichità necessariamente disegnate con mezzi e su supporti rudimentali, ma anche quelle di tempi relativamente moderni, non riproducono con esattezza i confini dei campi. Né lo potrebbero, dato che un errore di qualche percento, il minimo che possa accadere per riproduzioni in scala non troppo piccola, darebbe luogo a un errore assoluto sul campo difficilmente accettabile. Quello che occorre in questi casi è la conoscenza della forma e delle misure dell'oggetto (campo, edificio) che si descrive; sarà poi compito del geometra ripristinare sul terreno la precisione mancante nella carta. Lo stesso accade per il matematico, al quale l'accuratezza delle figure non è di nessun aiuto nelle dimostrazioni. Alla precisione delle operazioni sul terreno la geometria della carta sostituisce quella del processo mentale.
Nel passaggio inverso dall'esattezza logica a quella materiale, conseguente all'ampliamento di scala necessario per passare dal progetto alla sua realizzazione, tendere le funi rimane una delle operazioni principali ben al di là dell'antichità egizia e della Grecia classica. Essa si ritrova quasi inalterata nell'epoca moderna, superata per alcuni versi solo dall'invenzione e dal perfezionamento di strumenti ottici. E mentre sulla carta una perpendicolare si ottiene facilmente con l'uso della riga e della squadra, la stessa operazione sul terreno richiede, per poter essere condotta a termine con una certa precisione, procedimenti radicalmente diversi. Sul terreno la squadra non serve perché è troppo piccola rispetto alle dimensioni delle figure. Anche ammesso di avere una squadra perfettamente ad angolo retto, la perpendicolare che essa è capace di tracciare sarà lunga al più un metro, o giù di lì; se si vuole costruire un quadrato di trenta o più metri di lato, occorre prolungare questa retta di un metro fino a trenta volte tanto, un'operazione questa così imprecisa, da dare probabilmente risultati non migliori di quelli che si potrebbero ottenere valutando a occhio l'angolo retto.
 Queste considerazioni ci riportano di nuovo al problema iniziale: quali tecniche usavano gli agrimensori egizi per delimitare sul terreno dei campi quadrati? come facevano per ottenere un angolo retto?
Queste considerazioni ci riportano di nuovo al problema iniziale: quali tecniche usavano gli agrimensori egizi per delimitare sul terreno dei campi quadrati? come facevano per ottenere un angolo retto?
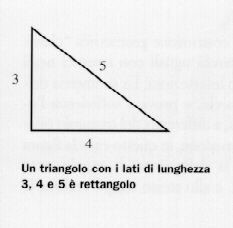
Un modo possibile, ipotizzato da vari studiosi, è legato alla conoscenza del teorema di Pitagora (VI sec. a. C.), o meglio del suo inverso, e cioè alla consapevolezza del fatto che un triangolo i cui lati hanno lunghezza 3, 4 e 5, nel quale quindi il quadrato del lato maggiore è uguale alla somma dei quadrati degli altri due, ha un angolo retto. Disponendo allora di una corda ad anello, di lunghezza totale 12, sulla quale siano segnati tre punti, a distanze per l'appunto 3, 4 e 5, e tirandola a forma di triangolo con i vertici nei punti segnati, si ottiene un angolo retto, e precisamente quello formato dai lati più corti, lunghi 3 e 4.
Se questo sia stato il procedimento effettivamente seguito dagli agrimensori dell'antichità non è noto, come non è certo che gli egizi sapessero che il triangolo di lati 3, 4 e 5 è rettangolo. Ma anche ammesso che essi avessero conoscenza di questo o di altri triangoli pitagorici (e ampie testimonianze della conoscenza di terne pitagoriche si hanno se non nella matematica egizia, certo in quella babilonese), resta il fatto che questa presuppone la conoscenza della natura, o quanto meno della generazione dell'angolo retto.
Da cosa proveniva questa conoscenza? In mancanza di documenti e di testimonianze anche parziali, proviamo ad affrontare il problema da un punto di vista differente, tramutandolo da storico in matematico. Chiediamoci allora: cos'è che rende un angolo retto differente dagli altri? ovvero, cos'ha di particolare l'angolo del triangolo di lati 3, 4 e 5?
Così posta. la questione ammette una risposta immediata: a differenza degli altri, i triangoli pitagorici, e in particolare il più semplice di questi, di lati 3, 4 e 5, si possono far combaciare ribaltandoli su un cateto, e poi di nuovo ribaltandoli sull'altro. Si ottiene così una configurazione simmetrica, che riempie tutto lo spazio disponibile senza sovrapposizioni e senza lacune.
 Nessun altro angolo oltre quello retto ha questa proprietà di simmetria; una caratteristica che nel primo testo di geometria ci sia pervenuto nella sua completezza, gli Elementi di Euclide (IV sec. a. C.), servirà come definizione:
Nessun altro angolo oltre quello retto ha questa proprietà di simmetria; una caratteristica che nel primo testo di geometria ci sia pervenuto nella sua completezza, gli Elementi di Euclide (IV sec. a. C.), servirà come definizione:
Quando una linea retta cadendo sopra un'altra retta fa angoli uguali, questi sono ambedue retti.
La natura dell'angolo retto risiede dunque nell'uguaglianza dei due angoli che si formano per il concorso di due rette, un'uguaglianza che nella geometria della carta può essere verificata immediatamente, piegando il foglio lungo una delle due linee concorrenti, e verificando che la seconda retta si ripieghi su sé stessa.
Alla stessa proprietà fa appello la costruzione geometrica "classica", consistente nel tracciare due cerchi, e unire le loro intersezioni. La simmetria della configurazione salta subito agli occhi, e prova a sufficienza l'uguaglianza dei quattro angoli. Di più, a differenza del triangolo pitagorico che richiede un'ulteriore costruzione, in questo caso la figura stessa suggerisce immediatamente la definizione di angolo retto mediante l'uguaglianza degli angoli, e allo stesso tempo realizza la sua costruzione.
Anche qui siamo comunque nel campo delle congetture. Di certo, il procedimento è semplice e di precisione notevolmente maggiore del precedente. Si potrà obiettare che in questo modo si traccia solo la perpendicolare che passa per il centro del segmento dato, o come si dice l'asse del segmento, ma non è difficile osservare che se si vuole ad esempio la perpendicolare in un estremo, come è necessario per tracciare un quadrato, basterà raddoppiare il segmento prolungandolo dalla parte dove si vuole tracciare la perpendicolare, e ripetere il procedimento precedente. Sarà necessario osservare che tutte queste tecniche si adattano particolarmente a un terreno piatto, come poteva essere la pianura egiziana?