Un museo per la matematica
| Il giardino di Archimede
Un museo per la matematica |
La geometria delle curve:
|
| |
| |
Sia la riga e il compasso, sia le sezioni coniche, fanno parte del patrimonio scientifico della Grecia classica, e in qualche modo lo compendiano. Si trovano, è vero, non poche altre curve nelle opere dei matematici greci: spirali, quadratrici, concoidi, cissoidi, anche in qualche caso curve spaziali, come le eliche di Pappo (III sec. d. C.) sulla superficie della sfera. Ma in ogni caso si tratta di curve particolari, provenienti più dall'immaginazione di questo o quel geometra che da una dinamica interna alla matematica, che invece va via via esaurendo la sua fioritura. L'apparire di queste curve speciali, più che indice di progresso scientifico, è il sintomo dell'inaridirsi di stimoli vitali in un virtuosismo in molti casi fine a sé stesso.
Tranne forse le sezioni coniche, tutte le curve della geometria greca sono curve "nominate". Ognuna di esse è definita per mezzo di proprietà caratteristiche valide per essa sola e nessun altra; ognuna ha bisogno di metodi ad hoc, che difficilmente possono trovare applicazione ad altre situazioni, legati come sono alla sua particolare generazione.
Per uscire da questo mondo chiuso occorre un punto di vista radicalmente differente, un metodo che si applichi a tutte le curve senza essere peculiare a nessuna, che privilegi la generalità a scapito della minuzia del procedere.
 Un passo decisivo consiste nell'introduzione delle coordinate cartesiane, che prendono il loro nome dal filosofo e matematico Réné Descartes (Cartesio, 1596-1650). Ogni punto P del piano può essere individuato per mezzo di due numeri (x,y), le distanze da due rette perpendicolari. Queste ultime si chiamano assi cartesiani, e i numeri x e y le coordinate cartesiane del punto P. Delle due, x si dice l'ascissa, e y l'ordinata del punto P. L'ascissa si prende positiva a destra e negativa a sinistra, l'ordinata positiva in alto e negativa in basso.
Un passo decisivo consiste nell'introduzione delle coordinate cartesiane, che prendono il loro nome dal filosofo e matematico Réné Descartes (Cartesio, 1596-1650). Ogni punto P del piano può essere individuato per mezzo di due numeri (x,y), le distanze da due rette perpendicolari. Queste ultime si chiamano assi cartesiani, e i numeri x e y le coordinate cartesiane del punto P. Delle due, x si dice l'ascissa, e y l'ordinata del punto P. L'ascissa si prende positiva a destra e negativa a sinistra, l'ordinata positiva in alto e negativa in basso.
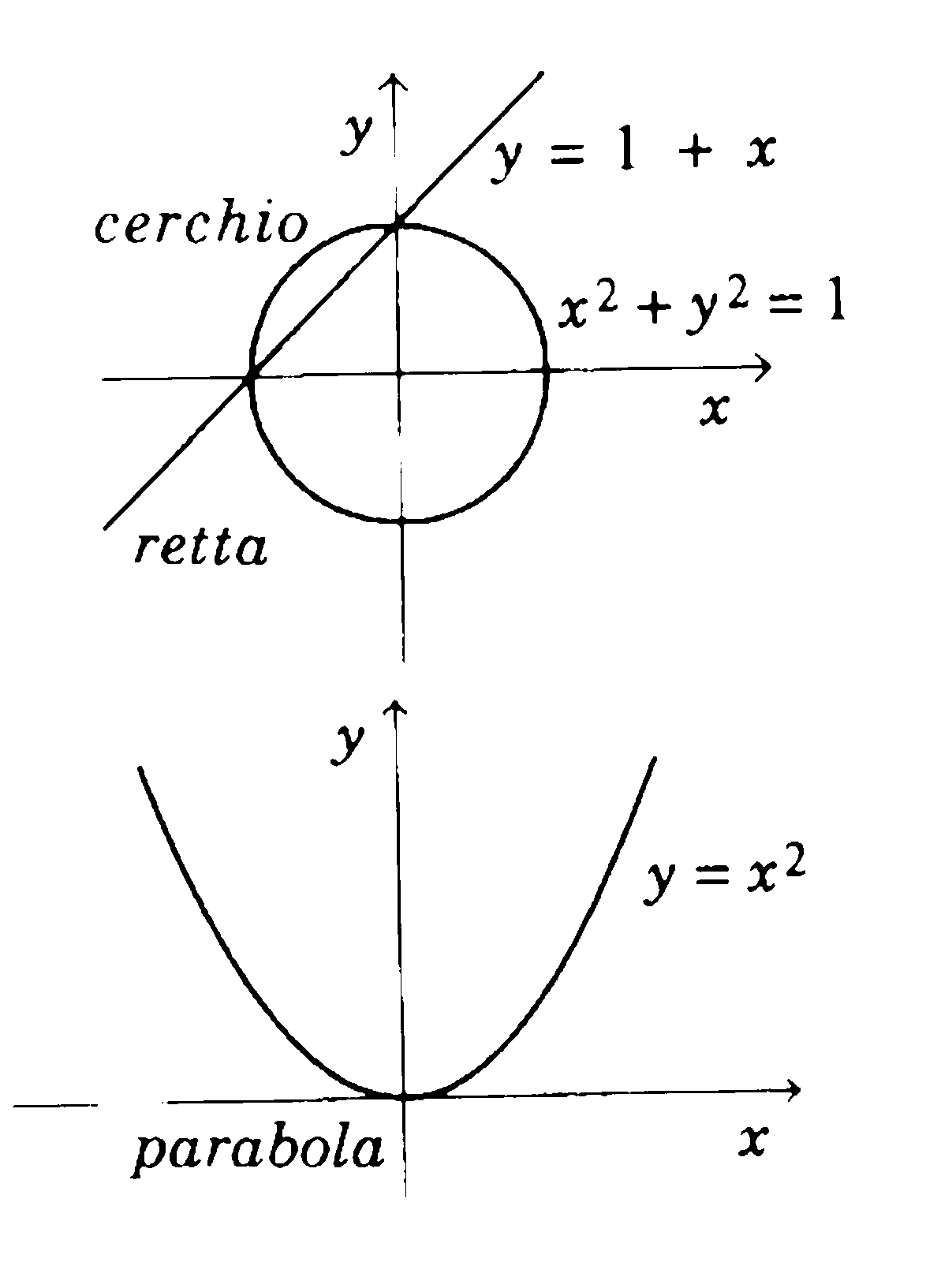
Quando le sue coordinate x e y variano in tutti i modi possibili, il punto P descrive tutto il piano. Se invece le coordinate di P sono legate da un'equazione, il punto corrispondente non potrà variare arbitrariamente nel piano, ma sarà costretto a seguire una curva. Così ad esempio l'equazione y=2 descrive una retta orizzontale, x2+y2=1 è l'equazione di un cerchio, y=x2 di una parabola.
In generale, a un'equazione algebrica F(x,y)=0, nella quale cioè F(x,y) è un polinomio nelle variabili x e y, si può collegare una curva, il luogo dei punti le cui coordinate (x,y) soddisfano l'equazione in questione. Quest'ultima può essere relativamente semplice, come quelle che esprimono una retta o un cerchio, ma anche piuttosto complicata, come ad esempio x27+y4-x3y13=1. Per mezzo di equazioni si potevano descrivere le curve più intricate: G. Bernoulli sosteneva che avrebbe potuto scrivere l'equazione del viso di un uomo.
Un metodo per ottenere i punti della curva consiste nel fissare il valore di una delle coordinate, ad esempio x=1, ottenendo in questo modo un'equazione F(1,y)=0, nella sola y. Risolvendo quest'ultima, si ottengono uno o più valori di y, che individuano uno o più punti della curva, in corrispondenza all'ascissa x=1. Prendendo poi valori diversi per la x si ottengono vari punti della curva, che può quindi essere tracciata con la precisione voluta.
Ad esempio, per costruire i punti dell'ellisse x2 + 4y2 = 1, si fissa x = a, e si risolve l'equazione a2+4y2 = 1. Le soluzioni di quest'ultima sono date da 4y2 = 1-a2, e quindi se -1<a<1 si hanno due soluzioni:
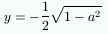 e
e
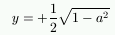 , mentre se a = 1 ovvero a = -1 si ha solo la soluzione y = 0, e se a>1 o a<-1 non si hanno soluzioni. Assegnando infine ad a valori diversi, compresi tra -1 e 1, e riportando su un grafico i punti corrispondenti, si ottengono una serie di punti della curva.
, mentre se a = 1 ovvero a = -1 si ha solo la soluzione y = 0, e se a>1 o a<-1 non si hanno soluzioni. Assegnando infine ad a valori diversi, compresi tra -1 e 1, e riportando su un grafico i punti corrispondenti, si ottengono una serie di punti della curva.
Il procedimento, si noterà, non è dei migliori se si vuole tracciare questa o quella curva particolare. Ad esempio, un cerchio può essere disegnato molto meglio e più facilmente con un compasso che non costruendo successivamente punti che verifichino l'equazione x2+y2 = 1. Lo stesso vale per l'ellisse, le sezioni coniche, e praticamente per tutte le curve particolari, per ognuna delle quali si può costruire uno strumento che la traccia più accuratamente e più rapidamente di quanto non si possa fare col metodo della determinazione successiva di dei suoi punti.
Questo però ha un vantaggio decisivo, quello di essere un metodo generale. È vero che per ogni curva si può inventare una macchina che la disegni, ma cambiando la curva si dovrà abbandonare il meccanismo usato per tracciarla e servirsi di un altro appositamente studiato per la nuova. Al contrario, il metodo del tracciamento per punti è indipendente dalla curva in questione, che entra solo con la sua equazione a differenziare un procedimento altrimenti uniforme. È proprio la possibilità di studiare metodi e procedimenti generali che rende la nuova impostazione cartesiana più agile e più potente rispetto alle tecniche costruttive della geometria classica.
Le curve possono dunque essere costruite per punti, risolvendo delle equazioni. Viceversa, le equazioni possono essere risolte per mezzo dell'intersezione di due curve.
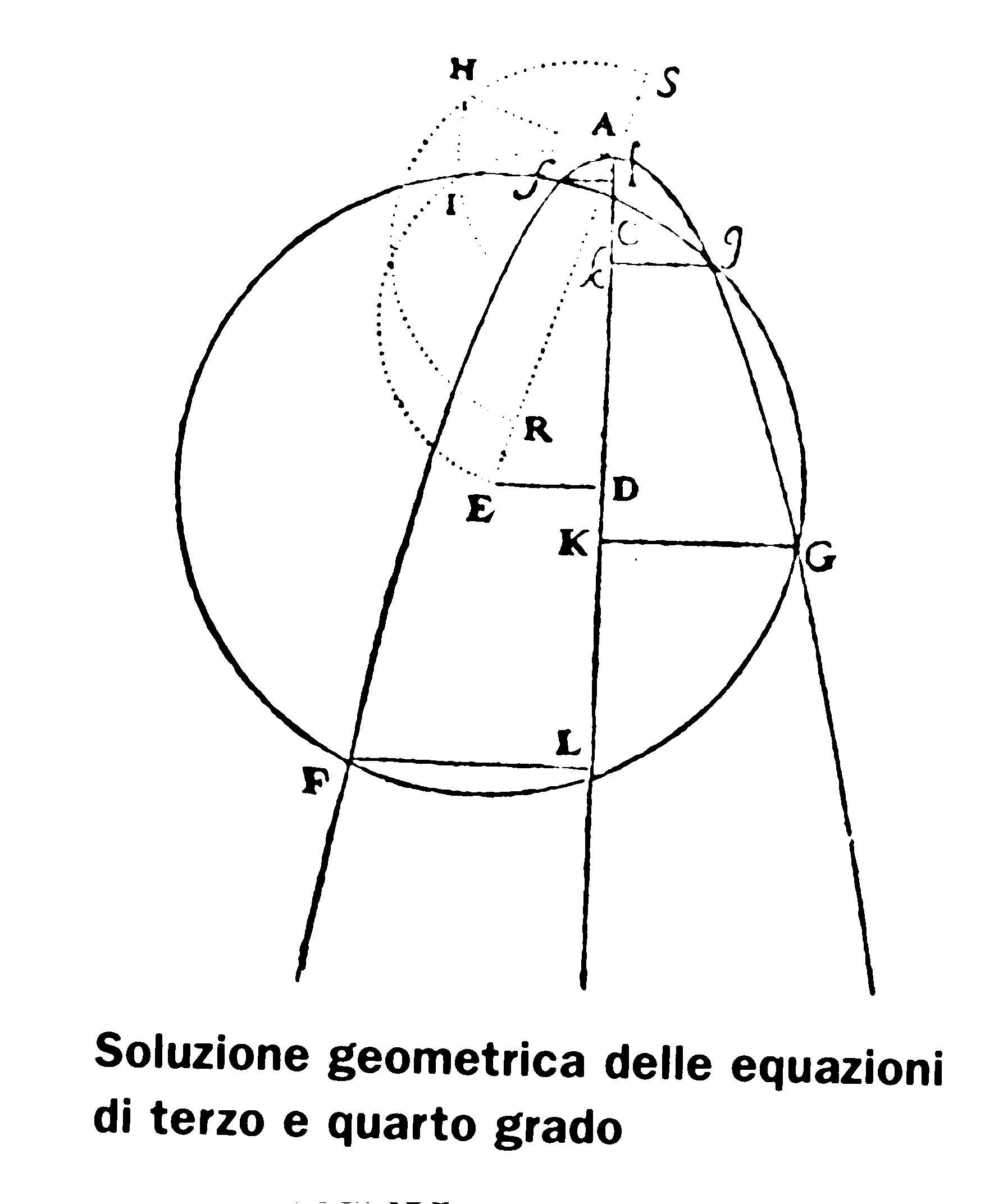 Se F(x,y) = 0 e G(x,y) = 0 sono le equazioni di due curve, i punti che appartengono all'intersezione di queste dovranno verificare ambedue le equazioni. Ora si può ricavare una delle due variabili, ad esempio la y in funzione della x, dalla prima equazione, e inserire il valore y(x) così trovato nella seconda, ottenendo in conclusione un'equazione P(x) = 0 nella sola x, le cui soluzioni sono le ascisse dei punti di intersezione delle due curve.
Se F(x,y) = 0 e G(x,y) = 0 sono le equazioni di due curve, i punti che appartengono all'intersezione di queste dovranno verificare ambedue le equazioni. Ora si può ricavare una delle due variabili, ad esempio la y in funzione della x, dalla prima equazione, e inserire il valore y(x) così trovato nella seconda, ottenendo in conclusione un'equazione P(x) = 0 nella sola x, le cui soluzioni sono le ascisse dei punti di intersezione delle due curve.
Se dunque si vuole risolvere l'equazione P(x) = 0, occorre trovare due curve F(x,y) = 0 e G(x,y) =0, tali che l'equazione data sia appunto quella risultante dall'eliminazione della y. Le ascisse dei punti di intersezione delle due curve danno le soluzioni dell'equazione.
Naturalmente, la stessa equazione P(x) = 0 si può ottenere con diverse scelte delle curve, o se si vuole delle funzioni F(x,y) e G(x,y). Così ad esempio le soluzioni x1 e x2 dell'equazione di secondo grado x2+x=4 si possono costruire intersecando la retta y = x con la parabola x2+y = 4, ovvero con l'iperbole xy+x = 4, o anche con il cerchio (x+1)2+y2 = 9, che ha il centro nel punto (-1,0) e raggio 3. Infatti, sostituendo il valore x al posto di y nell'equazione del cerchio, si ottiene (x+1)2+x2 = 9, ovvero 2x2+2x+1 = 9, da cui x2+x = 4. Tra tutte, si potrà scegliere quella che risponde a criteri di maggior semplicità, ad esempio l'ultima che fa intervenire solo una retta e un cerchio, e che dunque può essere costruita con riga e compasso.
Se il grado dell'equazione è maggiore di 2, le rette e i cerchi non bastano più, e si deve ricorrere a curve come le sezioni coniche o anche altre meno familiari. Ad esempio, le soluzioni dell'equazione x4+x2+3x = 1 si possono ottenere intersecando il cerchio x2+y2+3x =1 con la parabola y = x2. Via via che il grado dell'equazione diventa più elevato, saranno necessarie curve sempre più complesse.