Un museo per la matematica
| Il giardino di Archimede
Un museo per la matematica |
La geometria delle curve:
|
| |
| |
Gli sviluppi del calcolo infinitesimale nel diciottesimo secolo permettono di compiere notevoli progressi nello studio delle proprietà delle curve. Abbiamo già visto come, tra tutte le rette che passano per un punto P di una curva, la tangente sia quella che approssima meglio la curva nelle vicinanze di P. Se si vuole un'approssimazione migliore, dovremo andare al di là delle rette, e servirci di curve particolarmente semplici, ad esempio di circonferenze. Il procedimento è simile a quello usato per la retta tangente: tra tutti i cerchi che passano per P ce n'è uno che si adatta meglio all'andamento della curva nelle vicinanze di P. Questo cerchio, il cui centro si trova sulla retta perpendicolare alla curva (o, il che è lo stesso, perpendicolare alla sua tangente), prende il nome di cerchio osculatore.
Possiamo così misurare la curvatura di una curva. La retta tangente permette di determinare la direzione di una curva C: se si immagina un punto che si muove lungo C, si può pensare che ad ogni istante il movimento avvenga nella direzione della tangente. Analogamente la curvatura di C sarà data da quella del cerchio osculatore; e siccome un cerchio è tanto più curvo quanto minore è il suo raggio, si può misurare la curvatura di C per mezzo dell'inverso del raggio del cerchio osculatore, o raggio di curvatura.
Se si percorre una curva con velocità v, si è sottoposti a una forza centrifuga proporzionale a v2/r. Si vede allora che per non uscire di strada occorrerà diminuire la velocità nei tratti dove diminuisce il raggio di curvatura r, ovvero dove aumenta la curvatura; in altre parole si può andare più forte nelle curve larghe, ma bisogna rallentare in quelle strette. In un rettilineo poi non c'è forza centrifuga, dato che una retta ha curvatura zero.
Al variare del punto P sulla curva, i centri di curvatura (centri dei cerchi osculatori) descriveranno una seconda curva, che si chiama evoluta della prima. Questa curva è anche l'inviluppo delle rette perpendicolari alla curva data.
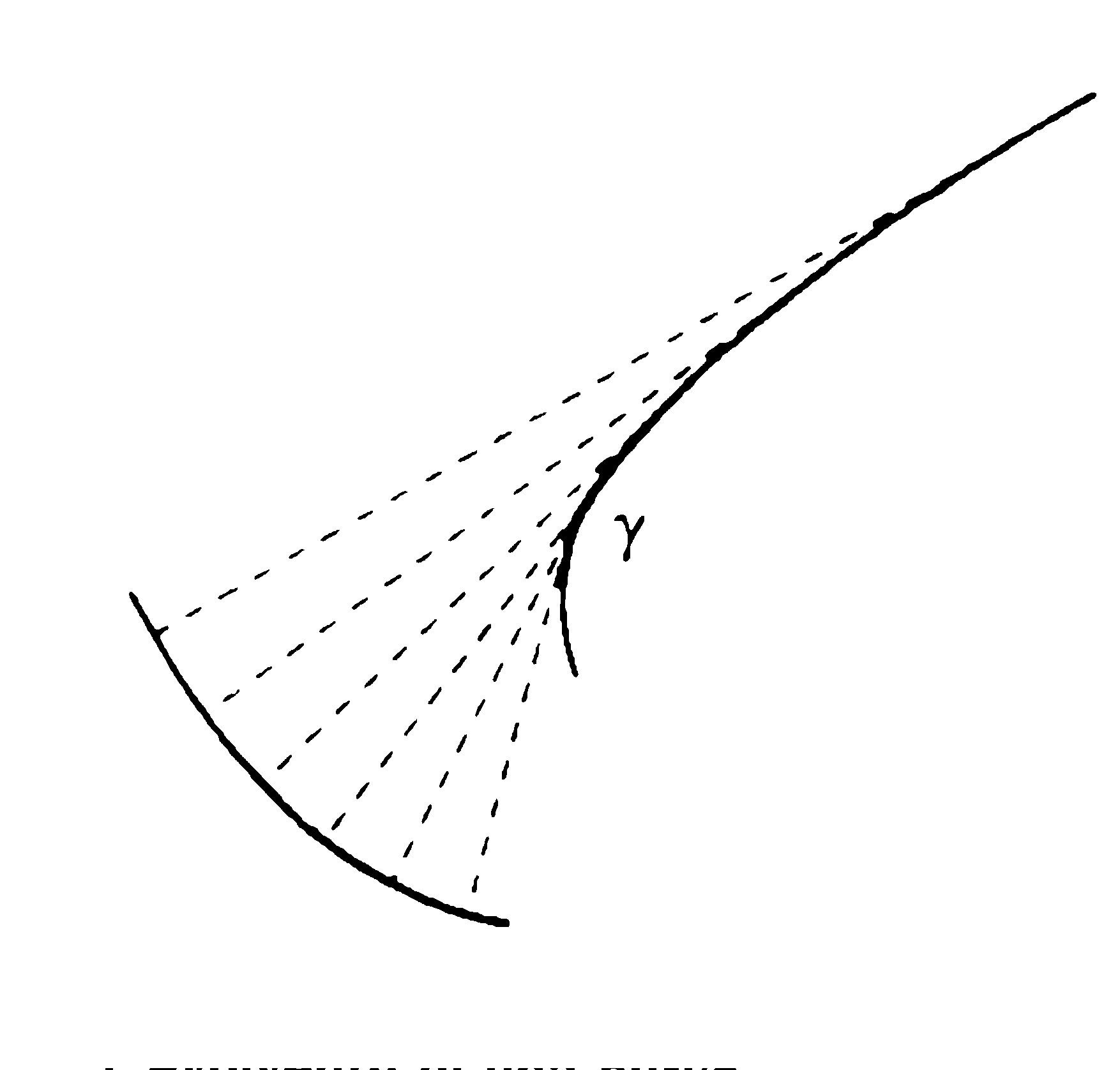 Reciprocamente, la prima curva è l'evolvente della seconda. L'evolvente di una curva C si può ottenere materialmente ritagliando una tavoletta secondo il profilo di C, attaccando un filo a questo profilo, e poi svolgendolo pian piano, con l'accortezza di tenere sempre tesa la parte staccata. L'estremità libera del filo descriverà allora l'evolvente di C.
Reciprocamente, la prima curva è l'evolvente della seconda. L'evolvente di una curva C si può ottenere materialmente ritagliando una tavoletta secondo il profilo di C, attaccando un filo a questo profilo, e poi svolgendolo pian piano, con l'accortezza di tenere sempre tesa la parte staccata. L'estremità libera del filo descriverà allora l'evolvente di C.
La relazione evoluta-evolvente può essere utile anche per risolvere problemi tecnici. Parlando delle oscillazioni abbiamo detto che un perfetto isocronismo si ha quando il moto si svolge lungo una cicliode. Naturalmente, l'isocronismo è importante nella costruzione degli orologi a pendolo. ma come si può fare per far muovere un pendolo lungo una cicloide? Si potrebbe costruire un profilo a forma di cicloide, e far rotolare il peso del pendolo lungo di questo, ma anche a non considerare la difficoltà di garantire un movimento regolare, l'attrito del peso lungo il profilo basterebbe a fermare il pendolo dopo pochi minuti. Se invece attacchiamo il peso a una cordicella che appendiamo per l'altro estremo, il pendolo descriverà un cerchio, che non è isocrono.
Il problema si risolve costruendo due guide, che si mettono dalle due parti del punto di sospensione; in questo modo il filo del pendolo non sarà libero di muoversi, ma dovrà seguire in parte la guida: l'estremità del pendolo descriverà allora l'evolvente del profilo. Si dovrà allora tracciare quest'ultimo in modo tale che la sua evolvente sia una cicloide, cioè a forma di evoluta della cicloide. Quest'ultima è ancora una cicloide, che è l'unica curva che sia evoluta ed evolvente di sé stessa. Costruendo quindi due guide a forma di cicloide si otterrà un pendolo perfettamente isocrono.