Un museo per la matematica
| Il giardino di Archimede
Un museo per la matematica |
La geometria delle curve:
|
| |
| |
La possibilità di considerare curve "generiche" pone in maniera differente molti problemi classici, in particolare quello delle quadrature e delle tangenti.
Quadrare una figura significa letteralmente trovare un quadrato equivalente alla figura data. Naturalmente, la soluzione di un problema di quadratura dipende dagli strumenti che riteniamo ammissibili nella costruzione del quadrato richiesto. Ad esempio, quando si parla del problema classico della quadratura del cerchio, si intende con riga e compasso. Così formulato, il problema è stato risolto solo nel secolo scorso, con la dimostrazione dell'impossibilità di una tale costruzione; se però si ammettono altri strumenti, come ad esempio la quadratrice di Ippia, il problema ha una risposta affermativa, nota fin dall'epoca greca.
 Se ci si limita alla riga e al compasso, ben pochi sono i risultati positivi: Ippocrate riesce a quadrare le lunule, il primo esempio di quadratura esatta di una figura curvilinea; Archimede scopre la quadratura della parabola. Similmente, i geometri classici avevano risolto in alcuni casi il problema delle tangenti, ovvero di determinare la retta che approssima meglio di ogni altra una curva data nelle vicinanze di un suo punto. I greci avevano determinato la tangente al cerchio o alle sezioni coniche, come pure ad altre curve particolari.
Se ci si limita alla riga e al compasso, ben pochi sono i risultati positivi: Ippocrate riesce a quadrare le lunule, il primo esempio di quadratura esatta di una figura curvilinea; Archimede scopre la quadratura della parabola. Similmente, i geometri classici avevano risolto in alcuni casi il problema delle tangenti, ovvero di determinare la retta che approssima meglio di ogni altra una curva data nelle vicinanze di un suo punto. I greci avevano determinato la tangente al cerchio o alle sezioni coniche, come pure ad altre curve particolari.
Nella nuova formulazione cartesiana, i due problemi prendono un aspetto diverso: non più quadrare questa o quella figura, o trovare la tangente a questa o quella curva, ma individuare un metodo uniforme, che permetta di tracciare la tangente a una curva arbitraria, o dare un procedimento per quadrare una figura delimitata da una curva qualsiasi.
Il primo di questi problemi, risolto in parte dallo stesso Descartes, condurrà alla scoperta del calcolo differenziale per opera di Newton (1643 - 1727) e Leibniz (1646 - 1716). Il secondo sarà l'oggetto del calcolo integrale.
Più difficile è il cosiddetto problema inverso delle tangenti, o in termini moderni l'integrazione di un'equazione differenziale.
Dal punto di vista geometrico, il problema consiste nel trovare una curva conoscendo una relazione tra i suoi punti e le tangenti relative. Analiticamente, esso si traduce in un'equazione che lega le variabili x ed y con i loro differenziali. Oltre che da problemi geometrici (come il cosiddetto problema di De Baune, il primo ad essere formulato in termini di equazioni differenziali) queste equazioni conducono alla soluzione di non pochi problemi di fisica, e in particolare di meccanica, in primo luogo quello di trovare la traiettoria di un corpo soggetto a una data forza. Di questo tipo sono la caduta dei gravi, e in genere il moto di un corpo nel vuoto o in un mezzo resistente, e la determinazione delle orbite dei pianeti, soggetti a una forza attrattiva proporzionale all'inverso del quadrato della distanza dal sole. Ambedue questi problemi sono affrontati da Newton nei suoi Principia; pochi anni più tardi Leonhard Euler (1707-1783) sottometterà al calcolo tutta la meccanica.
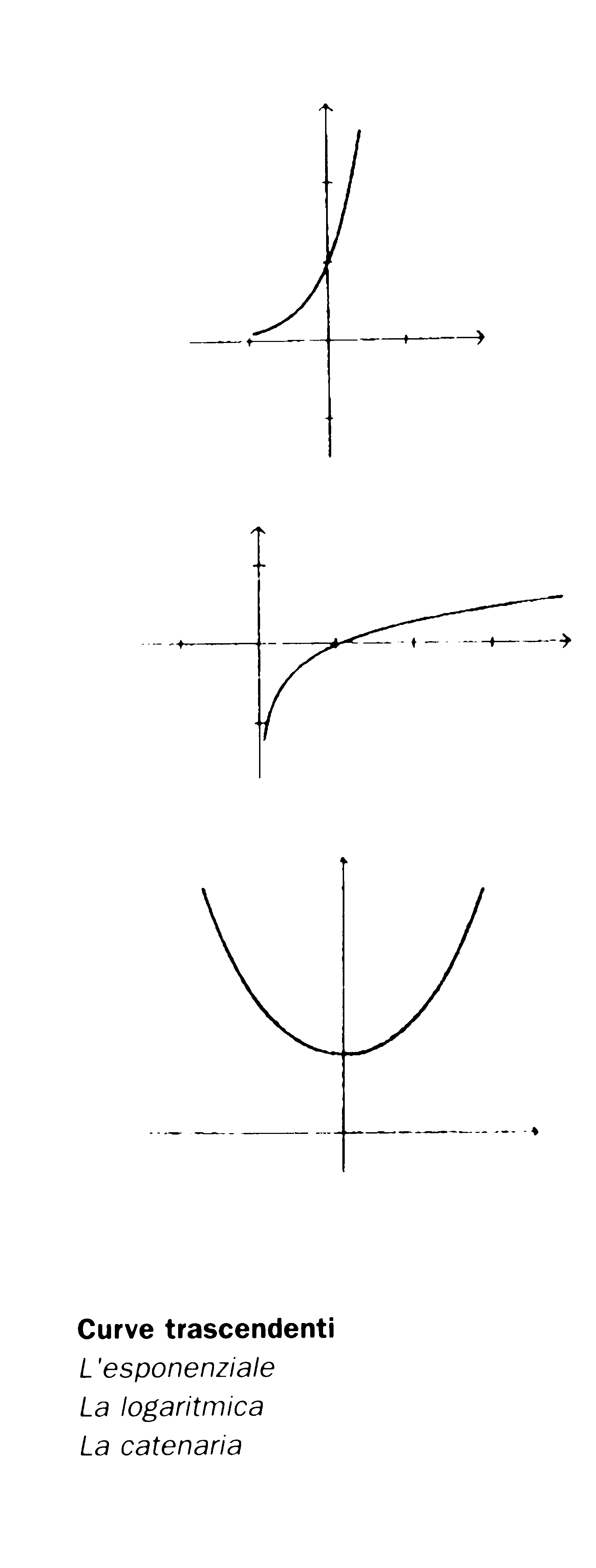
Le equazioni differenziali portano alla ribalta una nuova classe di curve, che erano emerse solo sporadicamente nel corso del diciassettesimo secolo: le curve trascendenti. Si tratta di curve che non si possono esprimere mediante un'equazione algebrica, ma richiedono per essere descritte analiticamente l'introduzione di nuove funzioni, tra cui le funzioni trigonometriche, i logaritmi, gli esponenziali.
Già il primo problema riconducibile a un'equazione differenziale, il problema di De Baune, ha come soluzione la curva esponenziale, di equazione y = ex. La stessa curva, vista scambiando tra loro i due assi, e di equazione x= log y, interviene nel problema della quadratura dell'iperbole. Via via che vengono affrontati nuovi problemi, insolubili prima dell'invenzione del calcolo, si scoprono nuove curve trascendenti. Il primo problema affrontato con successo è quello della forma di una catena appesa agli estremi: esso ha come soluzione una curva, la catenaria, di equazione
y = (ex+e-x)/2.
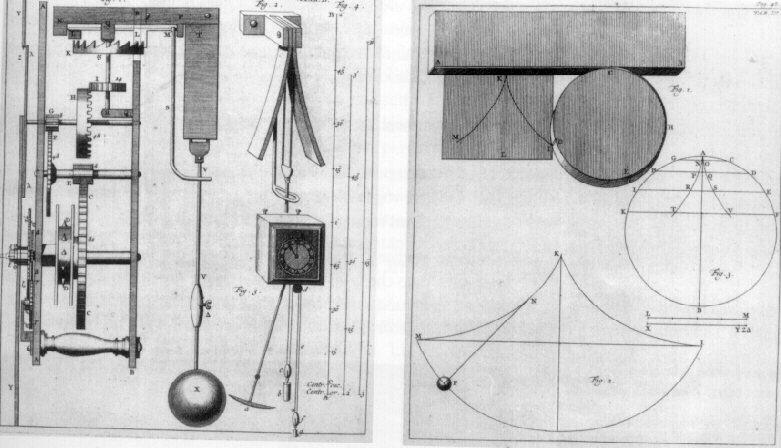
Un secondo successo del nuovo calcolo è la determinazione della brachistocrona, la curva che rende minimo il tempo di caduta da uno dei suoi estremi all'altro.
Più precisamente, supponiamo di fissare due punti P e Q, il primo posto più in alto del secondo, ma non sulla verticale, e lasciamo cadere da P un grave che giunga a Q scivolando su una curva che unisce i due punti. Poniamoci ora il seguente problema: tra tutte le curve che uniscono P e Q, qual'è quella che rende minimo il tempo di caduta? Non è, come potrebbe sembrare a prima vista, la retta che unisce i due punti; infatti per diminuire il tempo di caduta conviene iniziare quasi verticalmente, in modo da acquistare subito velocità, anche a scapito della maggior lunghezza del cammino.
In questo caso, la soluzione è una cicloide, la curva descritta da un punto di un cerchio che rotola senza strisciare.
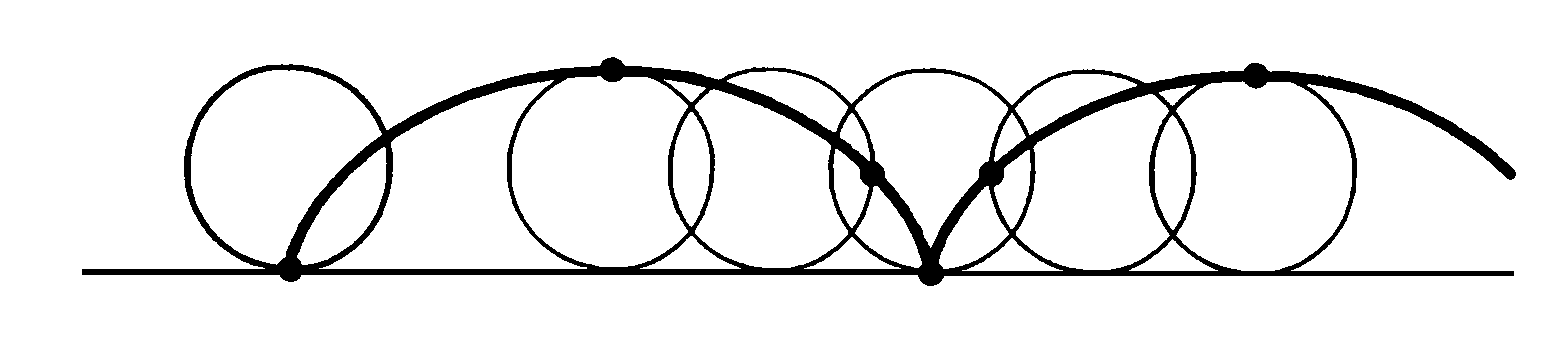
La stessa curva fornisce la soluzione anche di un altro problema. Supponiamo di poggiare una pallina su un profilo a forma di semicerchio e di lasciarla andare. La pallina comincerà ad oscillare avanti e indietro, mentre il tempo che impiega a fare un'oscillazione completa andrà diminuendo via via che diminuisce l'ampiezza dell'oscillazione, restando quasi costante per oscillazioni piccole. Ci si può allora chiedere: esiste una curva sulla quale tutte le oscillazioni, grandi e piccole, si svolgano nello stesso tempo? La risposta è affermativa: la curva isocrona è ancora la cicloide.