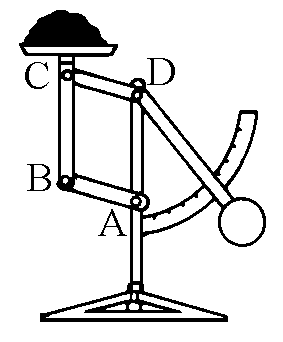
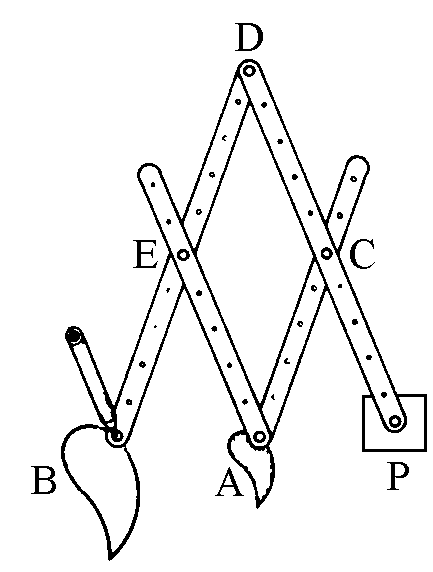
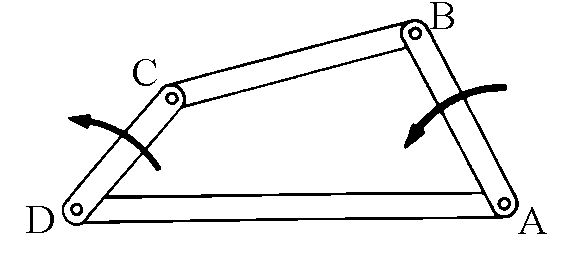
In everyday life one often encounters mechanisms of various kinds made of fixed axles hinged to each other or one sliding on the other .

Just think about the simple devices to open doors or windows, bicycle brakes, staplers, scales, typewriters, drafting machines or the numerous devices in a car: suspensions, connecting rods of the engine, windscreen wipers, steering wheels, carburetors, not to mention a small sampler of all we encounter in the home or at work everyday. On the other hand the very structure of the human body and of vertebrates in general is made of bones (the axles) and joints (the hinges).

Simple mechanisms, made of fixed elements hinged or sliding, allowed the construction of machines that transfer or amplify human or animal energy, or natural forces ( like those produced by water or wind) or artificial (steam, electricity), permitting to make preordained operations saving energy and time and with characteristics of uniformity and precision. And it is just the intensive and generalised use of these mechanism that determined the development of the industrial production, employing machines that in turn were produced by other machines.

What do all these simple or complex mechanisms have in common? To start with, each of them involve moving parts. Such parts interact with each other so to convert one type of movement into another. For example in the simple mechanism of a lock, turning the key one way or the other makes the bolt coming out or getting back in its place: a rotational movement is transformed into a translational one.

During the movement, the key points of the mechanism, meaning the pivots or the slides, describe more or less complex curves depending on the function performed. Think about the pantograph: if P is fixed and the point A describes a curve that has the same shape of the first one but is enlarged twice. By varying the length of the axles, the new curve can be reduced or enlarged by different factors in respect to the first one. The mechanism transforms a curve into another curve.

Thinking carefully about it, this fact is true for all mechanisms, even those made to draw curves, even those where the functioning does not appear to be, at first sight, slightly connected to any curve. If one point of the mechanism follows a "simple" path then another point can describe a path much more complex or difficult to obtain directly, so that one would like to say that a mechanismis a device that transforms a curve into another. The interest and the importance of these rods, mechanisms, articulated devices, or any way we want to call them, consist in the fact that they make one of their given points move along an appropriate curve without the profile of this last one being present. On the other hand, the same agility and versatility of our hand, from which our creativity partly derives, depends on a complex articulated mechanism through which we can not only trace with a pencil a curve or a figure that exists only in our imagination, while it is not at all intrinsic in the articulations, but we can turn a key, tighten a pair of pliers, and make a tennis racket describe a wanted trajectory.