|
Curves and mechanisms
F. Conti
(from the catalogue of the exhibition)
What is a mechanism ?
The problem of
rectilinear motion without friction
Watt's mechanism
Tchebycheff's
mechanism
Peaucellier's inverter
Hart's connecting rod
mechanism
Curves, connecting rod mechanisms and profiles
The
articulated quadrilateral and some applications
|
|
Peaucellier's inverter
|
|
The exact solution to the problem of rectilinear
motion was found in 1864 by Peaucellier and, published as
letter to the journal Nouvelles Annales de
Mathématiques,
it went nearly unnoticed. In 1871,
Lipkin independently found the same solution, and was
greatly honoured by the Russian government for the
supposed originality of his invention. Although
belatedly, Peaucellier's merit was recognised and he
received the important Montyon prize from the Institute
of France. For a complete picture of this discovery, we
must remember that as early as 1853 Sarrus had already
described a three-dimensional solution.
|
|

|
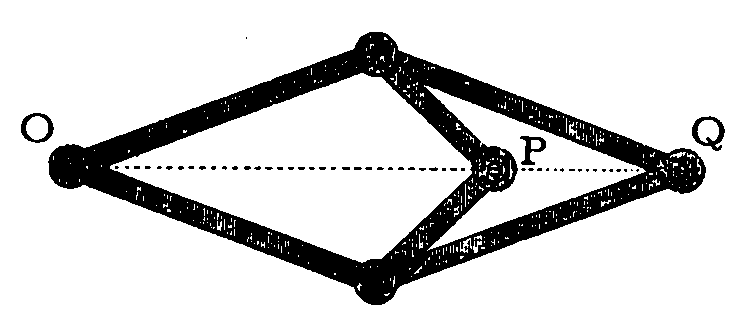
Let us then describe Peaucellier's discovery. His
mechanism is constituted by seven connecting rods. Four
of these, of the same length, form a rhombus, two longer
ones are connected to two opposed vertices of the rhombus
and between us in a fixed point O. The apparatus thus
described is known as the Peaucellier cell,
and
it has as a notable property that the P and Q points
correspond in a circular centre inversion O, that is the
distances OP and OQ are such that
OP · OQ = constant.
A
property of circular inversion, easy to demonstrate for
anyone with a minimal familiarity with Euclidean
geometry, is that the circles that pass through the
inversion centre (in our case point O) are sent into
straight lines. This explains the functioning of Peaucellier's
mechanism: if one adds a seventh rod which forces P to
draw a circle through O, then the point Q will draw a
straight line. A true straight line, not an approximation.
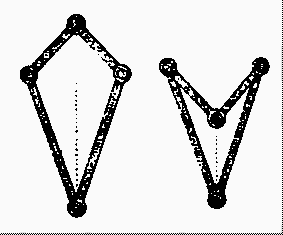
Peaucellier's cell can be obtained from the two
articulated quadrilaterals that appear in the figure on
the side, to which tradition has given the names kite
and arrow, superimposing them and identifying
the longer rods. If the same operation is executed
identifying the shorter rods, we obtain the mechanism in
the next figure.
In this case OQ · PQ = constant
and
if Q is forced to draw a circle through O then P will
move in a straight line.
"
In this very compact form, the mechanism has
been successfully applied to the machines used to
ventilate [London's] Houses of Parliament. The smoothness
of movement due to the absence of noise and friction is
really remarkable. The machines were built on the basis of
Peaucellier's mechanism by Mr. Prim, engineer of the
Houses of Parliament, to whose courtesy I owe the chance
of having seen them: I assure you they are worth a
visit." Thus the English mathematician
Kempe, wrote in 1877 in his interesting booklet How To Draw a
Straight Line. Unfortunately these ventilation
machines were destroyed, and it was not possible to
recover any documentation.
|
|
|
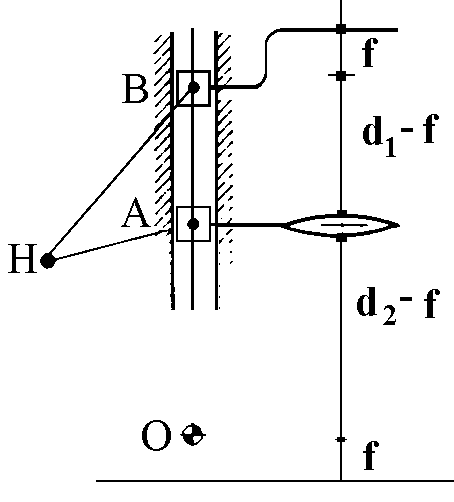
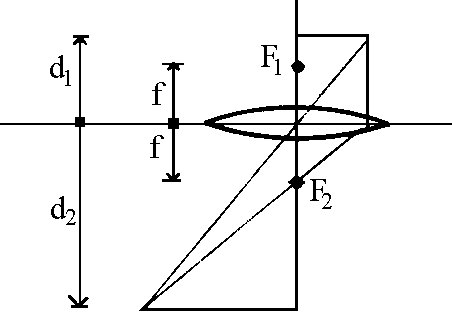
An interesting application of Peaucellier's cell is
found in autofocus photographic enlargers. If we consider
a lens with a focal distance f, foci F1,
F2, if d1, d2, are the
distances of the lens from the figure to be enlarged and
from the enlarged figure, one must have:
1/d1 + 1/d2 = 1/f
which is equivalent to:
(d1-f) (d2-f) = f2
This equation represents an inversion between the two
segments of length d1-f and d2-f
and must be respected for every height of the lens, if
one wants the projected image to always be in focus. Then
one can mount the lens and the negative holder on a
vertical support, perpendicular to the plane on which the
figure is projected. The alignment between the O, A, and
B mechanisms is then ensured and is therefore sufficient
to guarantee the inversion, one half of Peaucellier's
mechanism composed by two rods OH and BH of equal length,
connecting in the common point H with an AH rod. The
fixed point O is placed at a f distance from the
plane on which the image is formed, while the point B is
fastened to a negative-holding plane placed at a f
distance from point B itself. The condition above is
verified if one dimensions the rods such that OH2-AH2
= f2.
|
|
|
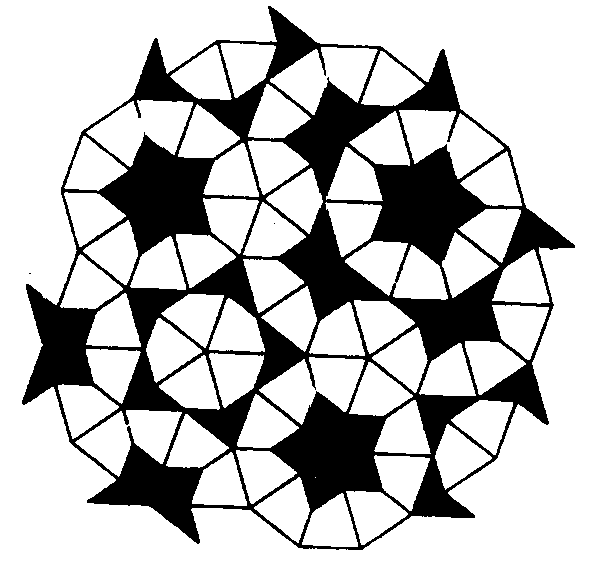
A last trivia, almost insignificant for us who speak
of mechanism but important in other contexts: in 1964 the
English physicist Penrose found that to determine the
length of the sides, Peaucellier's mechanism kite
and arrow configurations of Figure 7 can
constitute a non-periodic plane covering, that is one
that is not transformed in itself by any rigid movement
of the plane.
The study of these coverings has found an application in
near-crystal theory.
|
|
|