|
Curves and mechanisms
F. Conti
(from the catalogue of the exhibition)
What is a mechanism ?
The problem of
rectilinear motion without friction
Watt's mechanism
Tchebycheff's
mechanism
Peaucellier's inverter
Hart's connecting rod
mechanism
Curves, connecting rod mechanisms and profiles
The
articulated quadrilateral and some applications
|
|
The
articulated quadrilateral and some applications
|
|
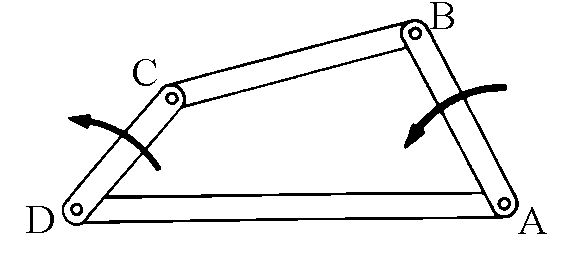
As we have seen, simple hinged rod
mechanisms can solve both theoretical and practical problems. The simplest of these mechanisms is
the articulated quadrilateral. If you
consider the ABCD quadrilateral with a fixed side AD, it
is clear that the position of one of the rods determines
that of the remaining ones. This mechanism has only
one degree of freedom.
If, in the version shown in the figure on side l, one
rotates the CD rod counter-clockwise, the AB rod also
begins to rotate counter-clockwise. However, at a certain
point the latter inverts its direction of motion,
although CD continues its counter-clockwise motion. It is
not easy to imagine the movement of this simple
mechanism - it's be best to make a simple model with
cardboard strips or Meccano rods or some such, or to
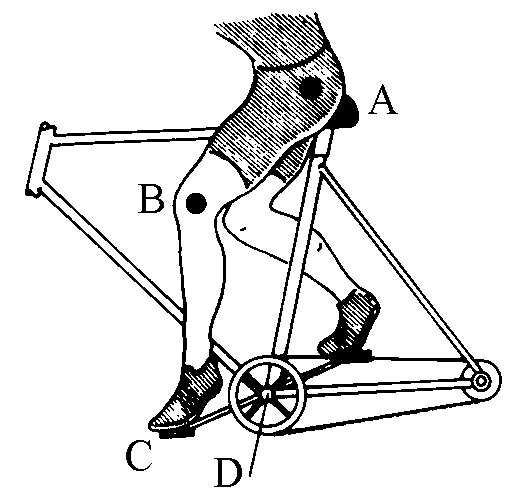
look at the figure on the side. The leg of the cyclist
and the arm of the pedal form an articulated
quadrilateral very similar to this one. The
difficulty in predicting the type of movement depends
also on the fact that, by varying the rods' length ratio,
the system may function in a very different way. This is
the fascinating, interesting and useful nature of the
articulated quadrilateral.
|
|
|
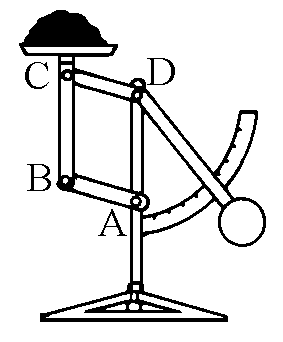
If the opposed rods are of equal
length, the system becomes an articulated
parallelogram, and the opposed rods always
remain parallel. This is the basis of numerous
applications of the mechanism which are under our eyes
every day. Drawing boards, scales, Venetian blinds, the
windscreen wipers of a bus (and of a cars, but in a less
obvious way) - all use this simple mechanism, which is
also found in some table lamps, in lifting machinery, in
bicycles gearboxes, in sewing baskets...
In each case in which it is necessary that some parts
keep a prefixed position on a plane, the articulate
parallelogram offers the optimal solution. For example,
in the case of the machinery used to lift personnel to
check street lighting, it is necessary to ensure that the
cabin stay horizontal, no matter the height from the
ground. Please note that some of the described examples
use two coupled parallelograms - in this way one may
obtain movements in two directions (with two degrees of
freedom) but the parallel nature of movement remains
guaranteed.
|
|
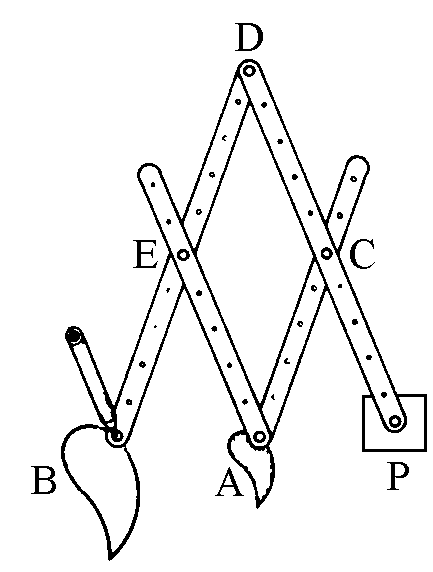
|
The pantograph is
itself practically based on a double articulated
parallelogram (in the case of Figure 1, it is a rhombus).
If PC = CD = DE = EB = AE = AC, then the points P, A, B
are always on a straight line and the distance of B from
the fixed point P is always twice that of A, so that, if
A draws a curve, B draws a similar curve, augmented by a
factor of 2.
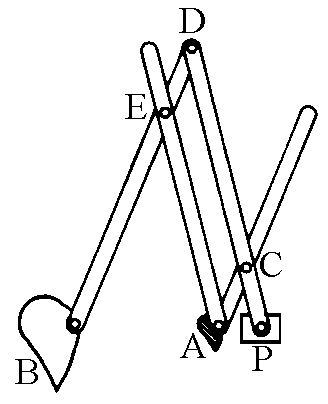
The figure on the side shows the diagram of a
pantograph in a configuration such that the
augmentation factor is four. Go back to the top of the page
In the general case, as we have seen, the
articulated quadrilateral works differently according to
the ratios between the rods' lengths. This is not the
time and place for a detailed analysis of the various
types. We will simply try to show the great versatility
of this mechanism. Often it is used as a force
multiplier, in the cases when the movement is caused by a
shaft rotating at near-constant speed, while the force
must be applied only on a short distance with small
movements, as it happens in oil-mills or in some cutting
devices. Or, on the contrary, this mechanism may be used
to transform alternating motion in circular motion, as in
the pedals of old sewing machines, or with even more
discreet functions, such as in rubbish bins.
|
|
|
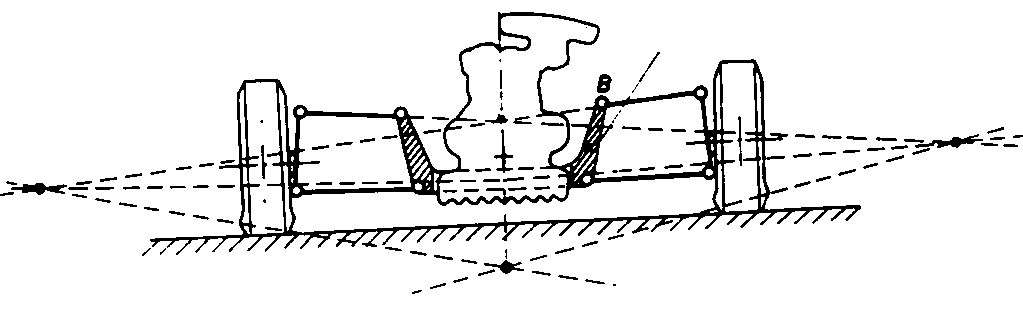
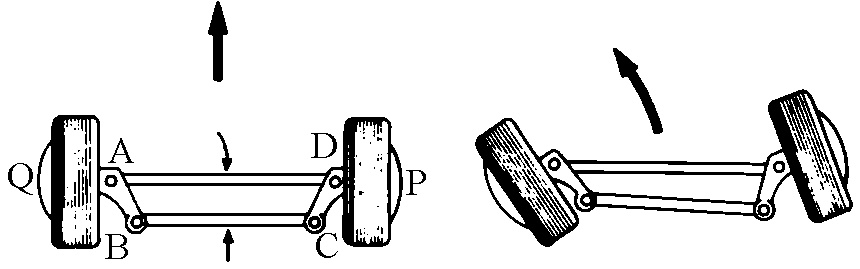
Also of interest is the use of the
articulated quadrilateral in the project for a car's
suspension (see figure) such that the wheels may absorb all the shocks due to the
road's irregularities, without directly transmitting them
to the passengers. In this case, one must ensure that
both wheels maintain the same vertical angle.

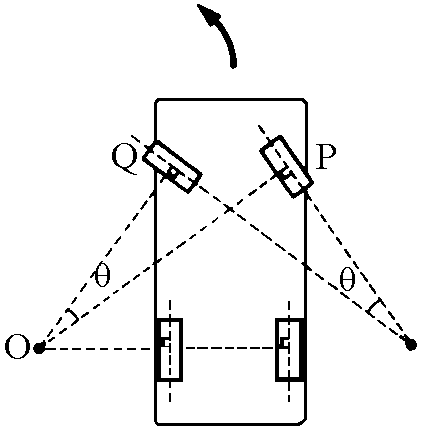
Even more
interesting is the use of the articulated quadrilateral
in car steering. The problem here is to allow the wheels
of a steering vehicle to have axes that go through the
same point, no matter the size of the steering radius. If
this condition is not met, the vehicle will lose its
stability in curves, and the tires will be under pressure from
lateral forces and will not be very durable. The solution was
found by the German engineer Ackermann in 1818, and
applied to horse-drawn carriages. It was perfected by
Jantaud and Panhard, on the basis of an articulated trapeze, and
it is described in the diagram.

|
|
|
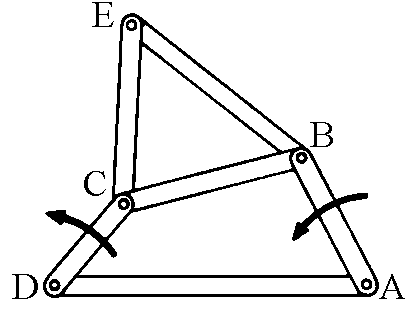
If one considers a
joint plane with the rod CB, leaving AD fixed and
rotating the shorter rod, the points of this plane draw
very diverse curves, according to the position of the
point. To individuate the point tracking the plane joint
to the BC rod, it is sufficient to add to the mechanism
other two rods BE and CE that form a triangle with BC.
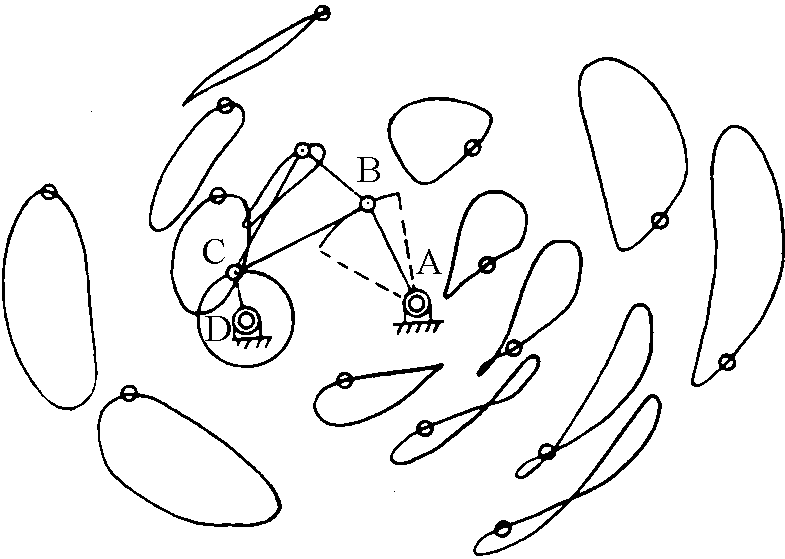
The following figure
gives an idea of this phenomenon: some curves are shaped
like a stretched 8, other are egg-shaped, other have an
almost rectilinear part.

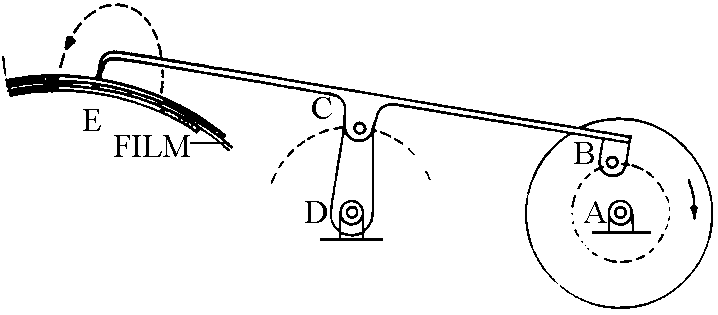
The latter opportunity is exploited e.g. in the film
pulling mechanism in motion picture projectors and
cameras (figure).
When B performs a full revolution around A, the point E
draws the dotted trajectory, causing the sudden
advancement of the film during its near-rectilinear part,
then frees itself and moves back on the other half of the
trajectory.

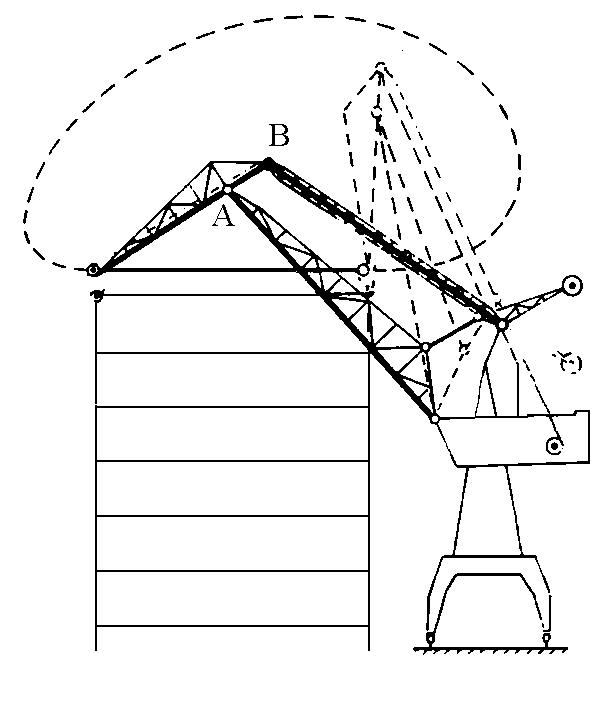
A crane's arms also takes advantage of
this property. In this case the problem lies in ensuring
that, varying the distance from the base, the height of
the load remains basically unchanged.
Obviously, more complex mechanisms can perform more
complex functions, but the problem there is not different
in principle from the simple cases which we have
analysed: what one wants to obtain from a mechanism is to
have a given point draw a given trajectory which
describes its function, without needing this trajectory
to exist physically.
As we have seen, Kempe has demonstrated that there
exists a connecting rod mechanism to trace any algebraic
curve. However, in general such a mechanism is
constituted by a very high number of rods. Having
determined more and more simple and functional mechanisms
to perform the same function, however approximately, has
been one of the fundamentals of technological progress.
|
|
|