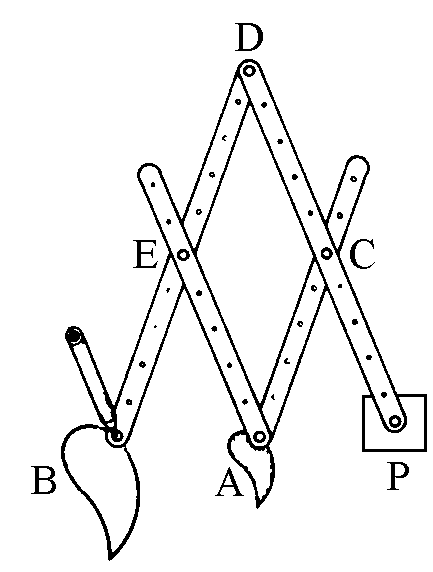
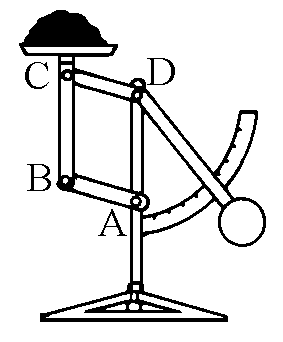
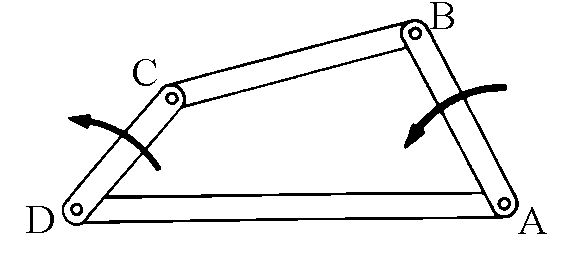
The simplest curves are doubtless the line and the circle. To draw circles, one uses a compass. It's sufficient to keep a constant distance between the tracing point and the centre, and one obtains a near-perfect circle, even with a primitive compass. At first sight, one would think that tracing a segment is also a very simple operation: you just need to use a ruler or pull a string taut. In fact, things don't work exactly like that. In order to draw a good straight line with a ruler, one needs the ruler itself to have a "straight" side, but the value of a ruled line depends on the ruler that was used to make it. So, who made the first ruler? To apply the same method to the circle would mean, for example, to take a coin and trace its edge - the circular profile would be "intrinsic" to the instrument itself.
It would be better to apply to the straight line the principle used to draw the circle, rather than viceversa. It may be worth noting that while the lathe is a very ancient machine (the lathe used by the Etruscan vase-makers was similar to the modern one), the line-maker, a machine made to produce the straightest possible profiles, appears only at the beginning of the industrial and technological revolution. It could not have been another way. The lathe produces conical, cylindrical or other circular shapes without requiring a cone, a cylinder or any other reference shape. The line-maker needs to have "of itself" a straight line or a reference plane as precise as possible. The construction of these "references" happens by progressive approximations, conceptually not dissimilar from passing over and over the plane - an instrument which appeared relatively recently.

There is, in other words, a substantial problem in tracing the simplest of curves, making the need to find an easy and accurate construction a daunting theoretical and practical problem.

The instruments on which Euclidean geometry is based, the ruler and the compasses are, therefore, not equivalent. Compasses are on themselves more precise than the ruler, and it would seem desirable to dispose of the latter. But in reducing the number of instruments available, it is reasonable to expect that the number of possible constructions will also diminish. The discovery by Mascheroni from Pavia in 1797, that any construction that can be obtained by ruler and compasses may be obtained with the compasses alone was surprising. By disposing of the ruler, the construction becomes more complex, but the result becomes more precise.
The interest of the problem lies not only in theory, as in many machines and apparatuses, one wants a point to move in a rectilinear direction with as little friction as possible. One of the problems which most challenged engineers at the end of the eighteenth and for part of the nineteenth centuries was that of finding an useful way of guiding the rod of a steam machine's piston into an alternated rectilinear motion. Without such a mechanism, the AB rod, which connects the piston rod to the motion collection wheel, would push the piston rod our of the vertical, quickly damaging the packing. On the other hand, the mechanism must have no rubbing parts, to avoid strong friction and a quick deterioration of the materials.