The importance of the problem of rectilinear motion in those days is witnessed by the over 150 articles that appeared during the nineteenth century on this topic, in journals of mechanics and mathematics. A great mathematician, the Russian Tchebycheff, who is credited with fundamental results in probability theory and in number theory, dedicated much energy to finding an "exact" solution to the problem. 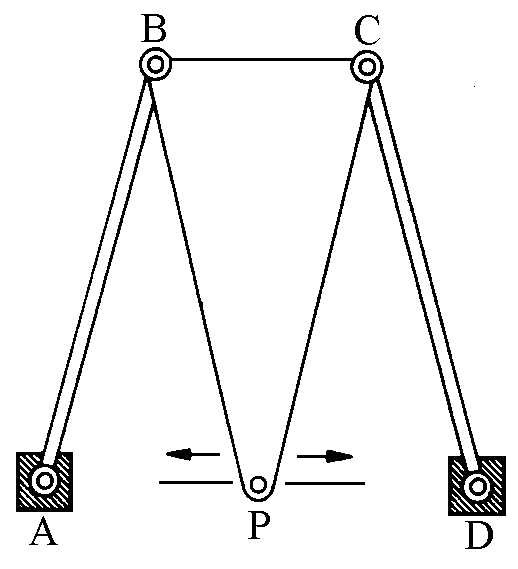In 1850, Tchebycheff managed to determine another approximated solution to the problem which may have been more accurate than Watt's, but was certainly less practical. It is based on a system with 3 connecting rods DA, AB, BC with C and D fixed, BC = AD and with distances such that AD : CD : AB = 5 : 4 : 2 . Around the symmetrical position shown in Figure 4, the median point P of AB draws a substantially rectilinear line (although the complete trajectory of P looks like a semicircle!). Sylvester writes that, after many fruitless efforts, Tchebycheff concluded that there existed no mechanism which could give an exact solution to the problem.
Tchebycheff's mechanism was used to drive the motion of the blades of timber saws.
It was a pupil of Tchebycheff, Lipkin, who found the mechanism that solves the problem in an exact manner, but he was preceded by Peaucellier, a French army officer whom we will discuss shortly.

n the meanwhile, the Englishman Roberts had proposed another approximate solution, based on a three-rod mechanism and on a BPC blade in the shape of an isosceles triangle. In this case one must have AB = BP = PC = CD and AD = 2 BC , the vertex P of the blade traces for a remarkably long tract a nearly straight line.