| |
|
|

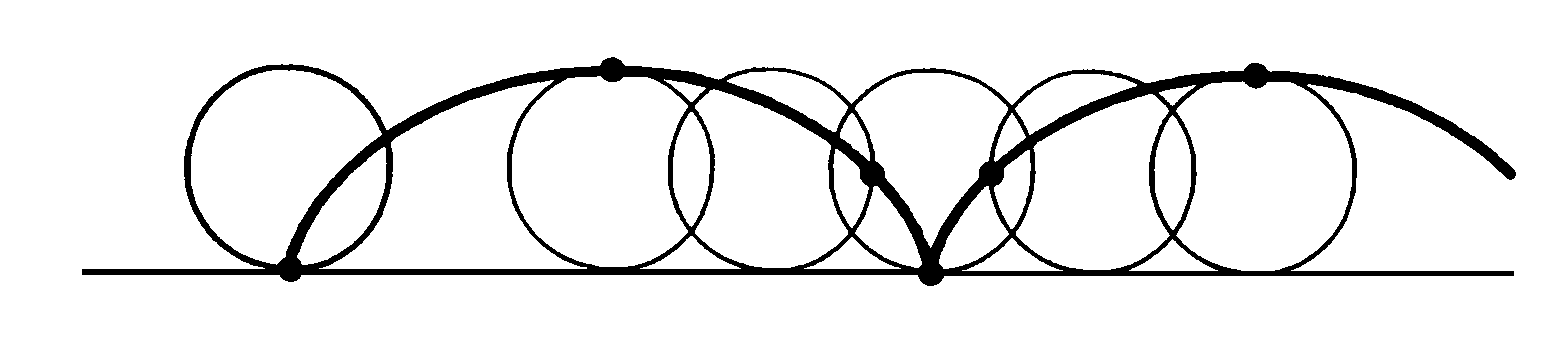 |
Let's mark the lowest point of a circle resting on a horizontal line.
If we move the circle along the line so that it rotates without friction,
the marked point will rise from the ground until it reaches
a maximum hight equal to the diameter of the circle. Then it it will sink
until it touches the ground, again at
a distance from the initial point that is equal
to the circumference of the circle. The curve described by the point,
which is repeated as we rotate the circle, is known as a
cycloid.
|
|