| |
|
|

|
At first sight, the figures referred to by the strange term fractals seem nothing more than
objects with heavily jagged contours. The nature of these intrinsically complex shapes is
revealed only when, enlarging them, one tries to examine their borders more closely.
Normally, when one enlarges the irregular
contour of a object - especially when dealing with a mathematically
defined shape - one expects to see the irregularity grow less as
one keeps enlarging, until it is revealed as an overall smoothness that
appeared irregular because of the scale discrepancy. None of
this happens with fractals. In fact, any change of scale
reveals new and surprising details that become more subtle and complex as each layer is revealed.
What initially seemed to be only a jagged profile,
is revealed upon inspection to be a fine, and extremely
diversified structure that branches off still further with each enlargement.
The irregularity of fractals is infinitely stratified. In spite of the
extreme variety of shapes, the generation of many of these objects
is very simple, requiring a computer program of only few lines.
|
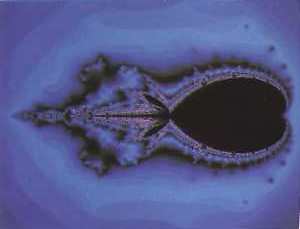
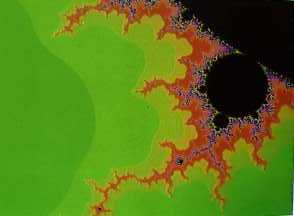

Set of Julia for transformation T(z) =
(1+i/2) sen z
 |
|
Let's imagine a powder placed on a flat surface. Its
particles can be moved on this surface, and they stay still
once we stop moving them. By spreading this material differently from
how its original arrangement, we operate a
transformation of the
plane. When the transformation has been effected, the particle that occupied the point P,
will occupy a different position, indicated with T(P) to
remind us that it is the
transformed of P.
For example, if P is
identified by its cartesian coordinates (x, y), we will be able to
describe the transformation T, saying what the coordinates
(x1, y1) of the point T(P) are, and that they will naturally depend on the coordinates of P:
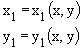
Suppose now we operate the transformation T for the second time.
The particle, originally in P, that was moved into T(P) will now
end up in a new point T (T(P)), or rather T2(P).
Transforming again,
and then again, the point will keep moving into 3(P), T4(P),and so
on, until, after a number of transformations, will be in Tm(P).
Let us now fix a circle W with a reasonably long radius and let us
ask ourselves this question: after how many transformations, will the
particle originally in P, get out of W ? Obviously, the
answer will depend on the initial position P of the particle. There
are vast areas, starting from which, the particle will get out of W
almost immediately. Other sectors of the plane, however, will
be particularily enduring in the sense that we will not see the
particle get out of W, within the maximum number of repetitions that
we have fixed.
This is the case with the simplest examples of the sets of Julia, that are obtained through transformation T, with only one fixed
point of attraction, PO All the points sufficiently near
PO are moved
into points even closer, while all the points sufficiently far
from the origin are moved into points even further away.
In this situation, all the points of the plane that aren't fixed
points of T, will fall into three distinct groups - those with images
growing apart indefinitely, those with images growing closer to PO
and the others, which have neither of these behavioural attributes, and which separate the two areas. This last set of points forms the
transformation
set of Julia and, because of a rather wide choice of
transformations, has a fractal structure.
In order to have an idea of such a structure we can operate in the
following manner. Having fixed a limited region W of the plane that
contains all the set of the points attracted by PO,for each point P
of W, we calculate a number of repetitions sufficiently high
order to get out of W, choosing for example the colour O (black) for
the points that remain confined in W.
As one would expect, if a point P requires N (as we shall assume)
repetitions to get out of W, the points to P will require a number
of repetitions near 50 (for example between 45 and 55). When, on the
other hand, we move into the areas characterised by a higher and higher N we'll see that the number of repetitions varies more and more rapidly,
passing from one point to another one next to it. This way, very
jagged figures are formed, where the colours are merged in
unpredictable, but never random, shapes. There is a method
to this madness. From these constantly new and unpredictable figures the beauty of fractals is derived.
|
|
|