|
SCHEDE DI APPROFONDIMENTO
Il teorema di Pitagora nell'estrema antichità
Una dimostrazione semplice
Un'altra dimostrazione semplicissima
Un triangolo non rettangolo
Parallelogrammi e trapezi
Figure simili
La diagonale del quadrato e gli irrazionali
Terne pitagoriche
I solidi regolari
|
|
Figure simili.
|
|
Nell’enunciato
del teorema di Pitagora, i quadrati possono essere sostituiti da altre figure, come ad
esempio triangoli, esagoni, o anche figure irregolari, purché simili tra loro.
|
|
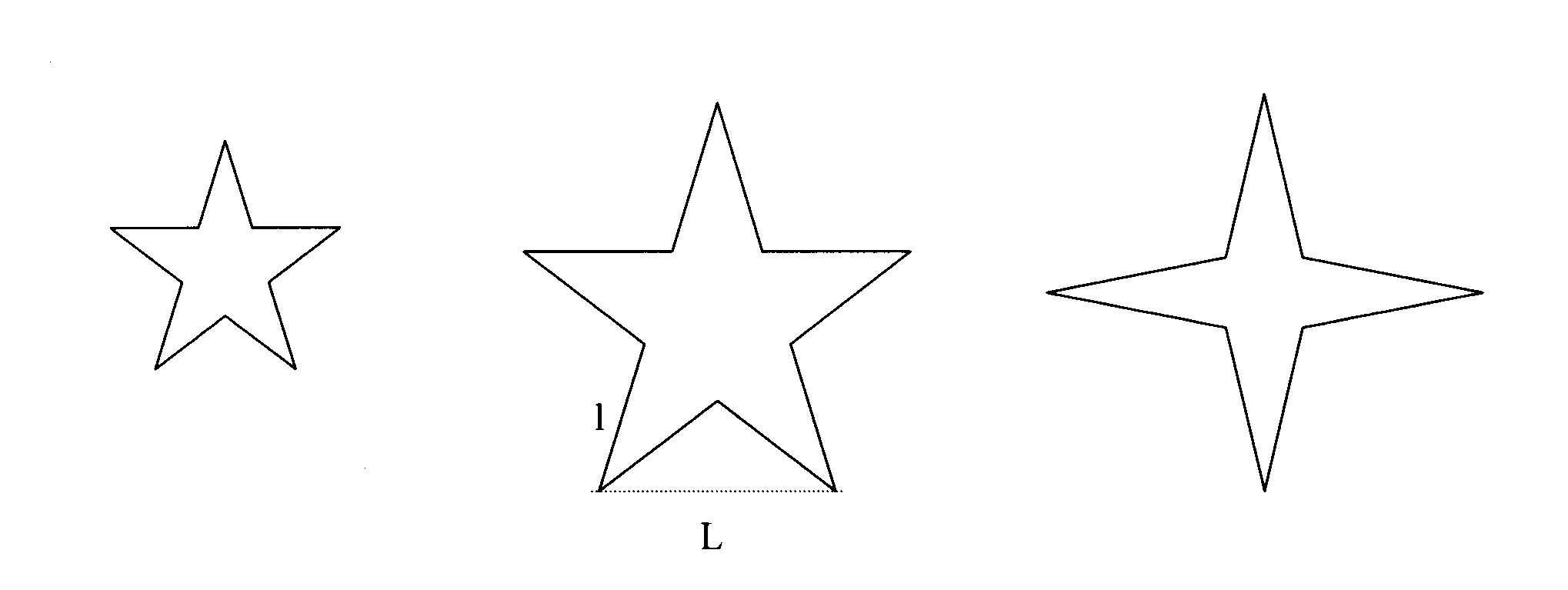
Le figure simili
sono quelle che differiscono solo per grandezza, ma non per forma. In altre parole, due
figure simili sono l’una l’ingrandimento dell’altra. Ad esempio, le due
stelle a cinque punte sono simili, mentre non sono simili una stella a cinque punte e una
a quattro punte.
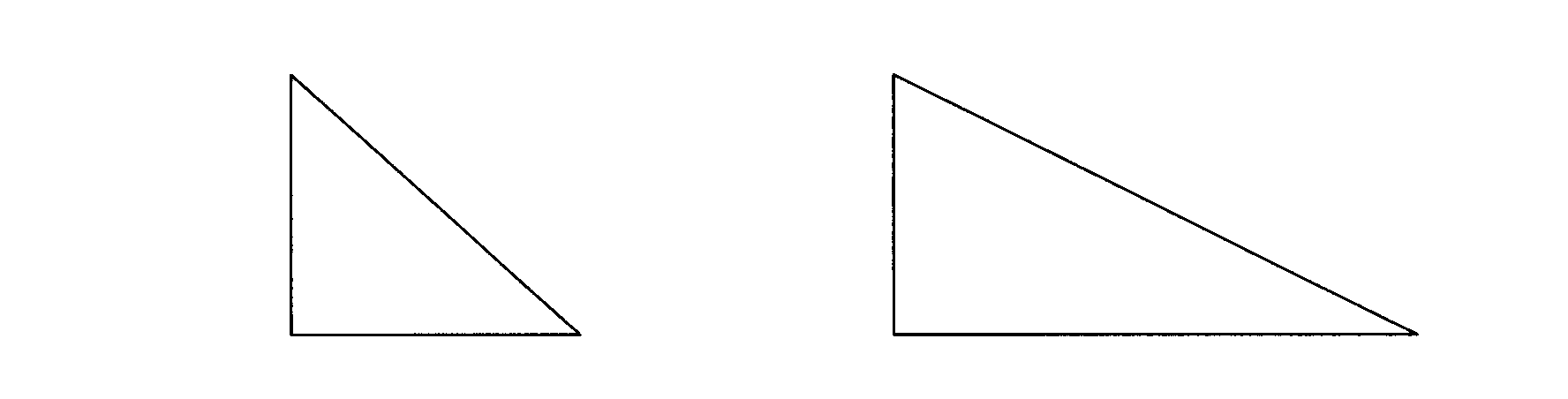
Analogamente, sono
simili due triangoli con i lati doppi l’uno dell’altro, mentre non lo sono
quelli in figura
perché in questo
caso l’ingrandimento si fa in una sola direzione. Osserviamo che tutti i quadrati
sono simili tra loro, come pure tutti i cerchi e tutti i poligoni regolari con lo stesso
numero di lati.
Una proprietà delle
figure simili, che spiega perché si possono sostituire ai quadrati nel teorema di
Pitagora, è che le loro aree sono proporzionali ai quadrati di segmenti corrispondenti.
Ad esempio, nel caso delle stelle a cinque punte, l’area è proporzionale al quadrato
della distanza tra due punte consecutive; in formule
A = kL2
(Naturalmente,
invece che la distanza tra due punte si sarebbe potuto prendere un lato l della stella; in
questo caso si avrebbe A =hl2 con una costante h diversa da k)
|
|
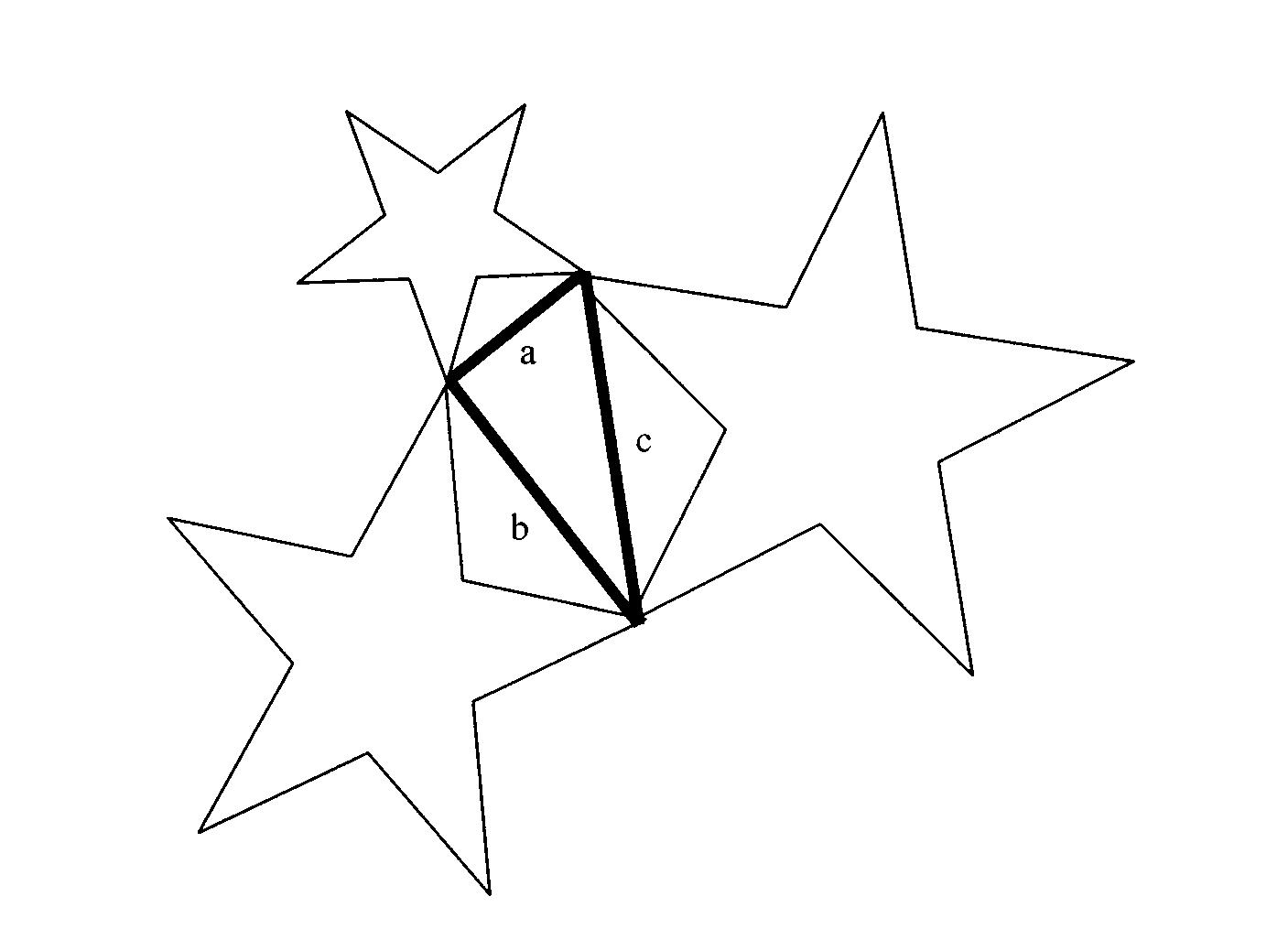
Se
ora prendiamo un
triangolo rettangolo, e adattiamo tre stelle ai suoi tre lati, come nella figura,
l’area della
stella sull’ipotenusa è uguale alla somma delle aree sui cateti.
Infatti per il
teorema di Pitagora si ha a2+b2=c2, e
moltiplicando per k, avremo ka2+kb2=kc2.
Ma per quanto appena detto, le quantità ka2, kb2 e kc2
sono le aree delle tre stelle, e quindi l’area della stella sull’ipotenusa è
uguale alla somma delle aree di quelle sui cateti.
|
|
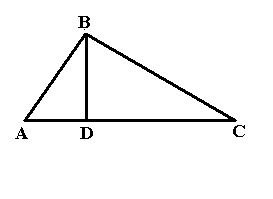
L’osservazione
precedente è alla base di un’elegante dimostrazione del teorema di Pitagora. Basta
osservare che i triangoli ABC e ADB nella figura sono simili, essendo rettangoli e avendo
in comune l’angolo in A. Per la stessa ragione risultano simili i triangoli ABC e
BDC, e quindi i tre triangoli sono figure simili
Poiché il triangolo
ABC è composto dagli altri due, la sua area è la somma delle aree di questi ultimi:
area (ABC) = area
(ABD) + area (BDC).
Siccome i triangoli
sono simili, le loro aree sono proporzionali ai quadrati delle loro ipotenuse, e quindi
k AC2
= k AB2 + k BC2
e dividendo per k
si trova
AC2 =AB2
+ BC2
cioè il teorema di
Pitagora.
|

 |
Lunule
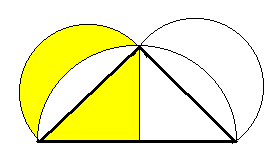
Un caso interessante
è quando le figure simili sono semicerchi. Ancora una volta la somma dei semicerchi sui
cateti è uguale al semicerchio sull’ipotenusa.
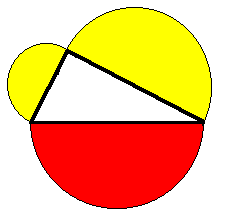
Se ora ribaltiamo
quest’ultimo, e togliamo sia al semicerchio grande che ai due piccoli le parti rosse
in comune, le figure che restano, cioè il triangolo e le due figure gialle a forma di
luna (che si chiamano lunule, dal latino lunulae, piccole lune), avranno
area uguale.
Se
poi il triangolo è isoscele, una lunula è uguale a mezzo triangolo. Questo è il primo
caso storicamente accertato (la dimostrazione
è attribuita a Ippocrate di Chio) in cui
si è dimostrato che una figura rettilinea (il triangolo) è uguale a una curvilinea (la
lunula).
|
|
|