Lunghezza e dimensione   

E oggi? I problemi connessi con le curve sono ancora numerosi, ma per lo più sono troppo tecnici per poter essere spiegati in poche parole. Uno però merita di essere descritto, anche se con qualche approssimazione, quello della dimensione.

La nozione intuitiva di dimensione di un oggetto ci dice che un corpo ha tre dimensioni, una superficie due, e una curva una. E in generale le cose stanno così; se si accetta che una retta ha una dimensione, una curva si può sempre rettificare, cioè ridurre a una retta senza cambiarne la lunghezza, e dunque ha anch'essa dimensione uno.

Vediamo le cose da un angolo leggermente differente: una curva si può costruire prendendo un segmento S e piegandolo come un filo di ferro fino a ottenere la forma voluta. Così facendo, ogni punto della curva proviene da un punto del segmento; si è ottenuta la curva come una rappresentazione parametrica di S. In questa operazione la lunghezza può rimanere la stessa, come avviene piegando un fil di ferro, oppure può variare, come avviene se disegniamo il segmento S su una superficie elastica, e poi lo deformiamo stiracchiando questa superficie. Ci sono, è vero, delle curve di lunghezza infinita, che si ottengono deformando non un segmento, ma una semiretta o tutta una retta; in ogni caso però è sempre possibile ridurle di nuovo a forma di una retta, in questo caso infinita. Tutte queste curve si chiamano rettificabili.

Ma è proprio vero che si può rettificare una curva qualsiasi? La risposta dipende da cosa si intende per curva. Se usciamo dalle curve familiari, e prendiamo il termine nella sua accezione più estesa, possiamo avere delle sorprese, come la celebre curva di Peano, scoperta (o inventata?) dal matematico torinese G. Peano (1858-1932).

Dividiamo un quadrato in quattro parti uguali, e tracciamo una spezzata come in figura; questa sarà la prima approssimazione della curva. La seconda approssimazione si ottiene dividendo ogni quadrato in quattro, e sostituendo le parti relative con delle spezzate un po' più elaborate. Di qui si prosegue, ogni volta dividendo in quattro tutti i quadrati, e in ognuno di questi ripetendo la sostituzione.

Tutte queste curve sono delle spezzate, la cui lunghezza va aumentando via via che si progredisce con la suddivisione. Quando si fa tendere il numero dei passi all'infinito, la successione delle spezzate "tende" alla curva di Peano. Quest'ultima non si limita ad avere lunghezza infinita, come è immaginabile dato che la lunghezza delle approssimanti cresce sempre più, ma addirittura riempie tutto il quadrato di partenza: la curva di Peano ha dimensione 2.

La curva di Peano può sembrare una di quelle astruserie spesso addebitate ai matematici, e per qualche verso è così, anche se serve a chiarificare il concetto di dimensione. Infatti essa fornisce l'esempio di un'applicazione continua (ma non biunivoca) tra un segmento e un quadrato. Si deve invece a G. Cantor (1845-1921) un esempio di applicazione biunivoca (ma non continua) tra un segmento e un quadrato; due esempi in certo modo simmetrici, che mostrano come per conservare la dimensione non basti avere trasformazioni biunivoche, né trasformazioni continue, ma che occorrano ambedue questi requisiti. In effetti si è dimostrato che la dimensione è un invariante topologico, e cioè si conserva per trasformazioni biunivoche e bicontinue.

Queste possono sembrare delle questioni puramente teoriche, mentre le curve che si incontrano nella realtà si comportano sempre con le dovute buone maniere. e invece la natura non è sempre così addomesticata come la si vorrebbe, e il problema della dimensione emerge anche in situazioni a prima vista del tutto mansuete

Supponiamo di voler misurare la lunghezze di un tratto di costa. Non potendo tirarla fino a farla diventare rettilinea, saremo costretti a usare qualche artificio, che ci darà, si spera, quanto meno una misura approssimata. Prendiamo allora un bastone lungo ad esempio un metro, e con un'estremità A all'inizio del tratto da misurare, ruotiamolo finché anche il secondo estremo B tochi la costa: e uno. Di qui ripartaimo tenendo fisso B e ruotando il bastone finché A vada di nuovo sulla linea della costa: due. Con un po' di pazienza, prima o poi arriveremo alla fine. Naturalmente, per avere un'idea della lunghezza potevamo usare una carta geografica e fare dei passi, diciamo di un chilometro. si sarebbe ottenuto un valore un po' meno preciso, ma certo con meno fatica.

I valori che abbiamo trovato sono tutti approssimati per difetto, avendo rimpiazzato tratti curvilinei con porzioni di retta. Naturalmente il valore che si ottiene dipende dalla lunghezza p del passo; in altre parole, non abbiamo ancora una lunghezza della costa, ma un numero L(p) che varia a seconda del valore di p. Quello che ci si aspetta è che, usando un passo sempre più corto, si ottengano dei valori di L(p) sempre maggiori, e che si avvicinino via via al valore "vero" della lungheza della costa.

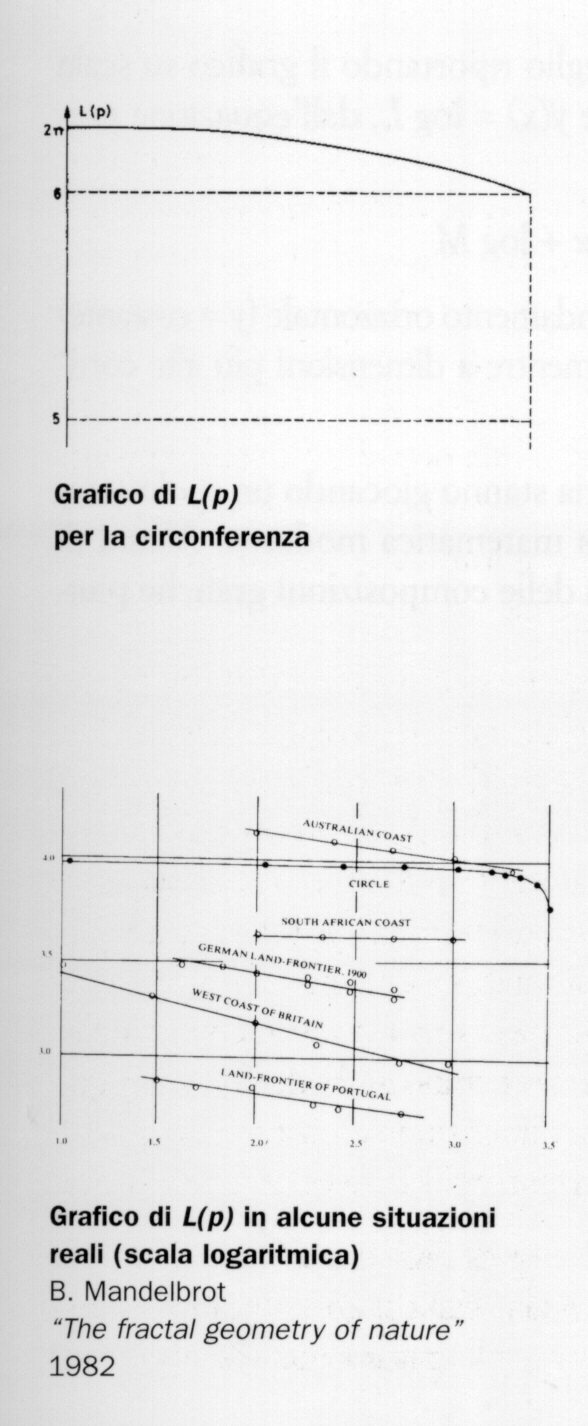
Effettivamente questo è quanto succede in alcuni casi artificiali, anche se l'andamento della lunghezza L(p) non è così regolare come si potrebbe immaginare. Ad esempio, se immaginiamo un'isola circolare, di raggio 1 km, e riportiamo in un grafico il valore di L(p) al variare di p da 1 km a 1 cm, otteniamo il grafico in figura. Quando p diventa molto piccolo, il valore di L(p) è vicino alla lunghezza della circonferenza 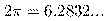km. Non solo, ma bastano valori piuttosto grandi di p per ottenere delle buone approssimazioni: già con p=1km si trova L=6km, (l'esagono inscritto), per p=100m si ottiene L=6.2806; se poi si prende p=1m si trova L=6.2832.

Lo stesso avviene per altre figure regolari. quando però si passa a misurare oggetti reali, si può andare incontro a delle sorprese: man mano che p diventa più piccolo, il numero L(p) continua a crescere senza dar segno di voler convergere verso un valore finito. anzi, dai grafici empirici la funzione L(p) sembrerebbe comportarsi come una potenza negativa di p:

Il numero D che appare nella formula precedente, e che ovviamente dipende dalla figura in esame, si chiama dimensione di Hausdorff in onore del matematico tedesco F. Hausdorff (1868-1942). Per le curve rettificabili, come la circonferenza o le sezioni coniche, risulta D=1 e L(p) tende verso la lunghezza della curva. In altri casi, D è un numero maggiore di 1, anche frazionario o irrazionale.

Naturalmente non è possibile dimostrare che un dato oggetto del mondo reale (ad esempio la nostra costa) ha dimensione diversa da 1. Infatti la definizione di dimensione dipende solo da cosa avviene per valori "e;piccoli"e; di p, e nella pratica nonj possiamo spingere le misure al di là di un qualche limite inferiore: se non altro perché a un certo punto interviene la strurrura atomica della materia che rende illusorio qualsiasi tentativo di misurare distanze troppo piccole. si può però affermare che, almeno alle distanze possibili, certe coste (ma anche alcune frontiere tra stati) si comportano come oggetti di dimensione maggiore di uno.

La costante D si vede molto meglio riportando il grafico su scala logaritmica. se si scrive x=log p e y(x)=log L(p),

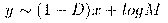
che è l'equaizone di una retta. Un andamento orizzontale (y=costante) caratterizza la dimensione D=1, mentre a dimensioni più alte corrispondono rette più inclinate

Oggetti di dimensione frazionaria stanno giocando un ruolo sempre maggiore in molti campi della matematica moderna. Alcuni di essi, i frattali, possono dar luogo a delle composizioni grafiche piuttosto affascinanti.