Se poi il piano della sezione passa per il vertice del cono, la sezione sarà un punto nel caso 1. e 2., una retta nel caso 3. e una coppia di rette nel caso 4. Così, intersecando un cono con un piano, si possono ottenere rette, cerchi, ed in più tre nuove curve, l'ellisse, la parabola e l'iperbole.
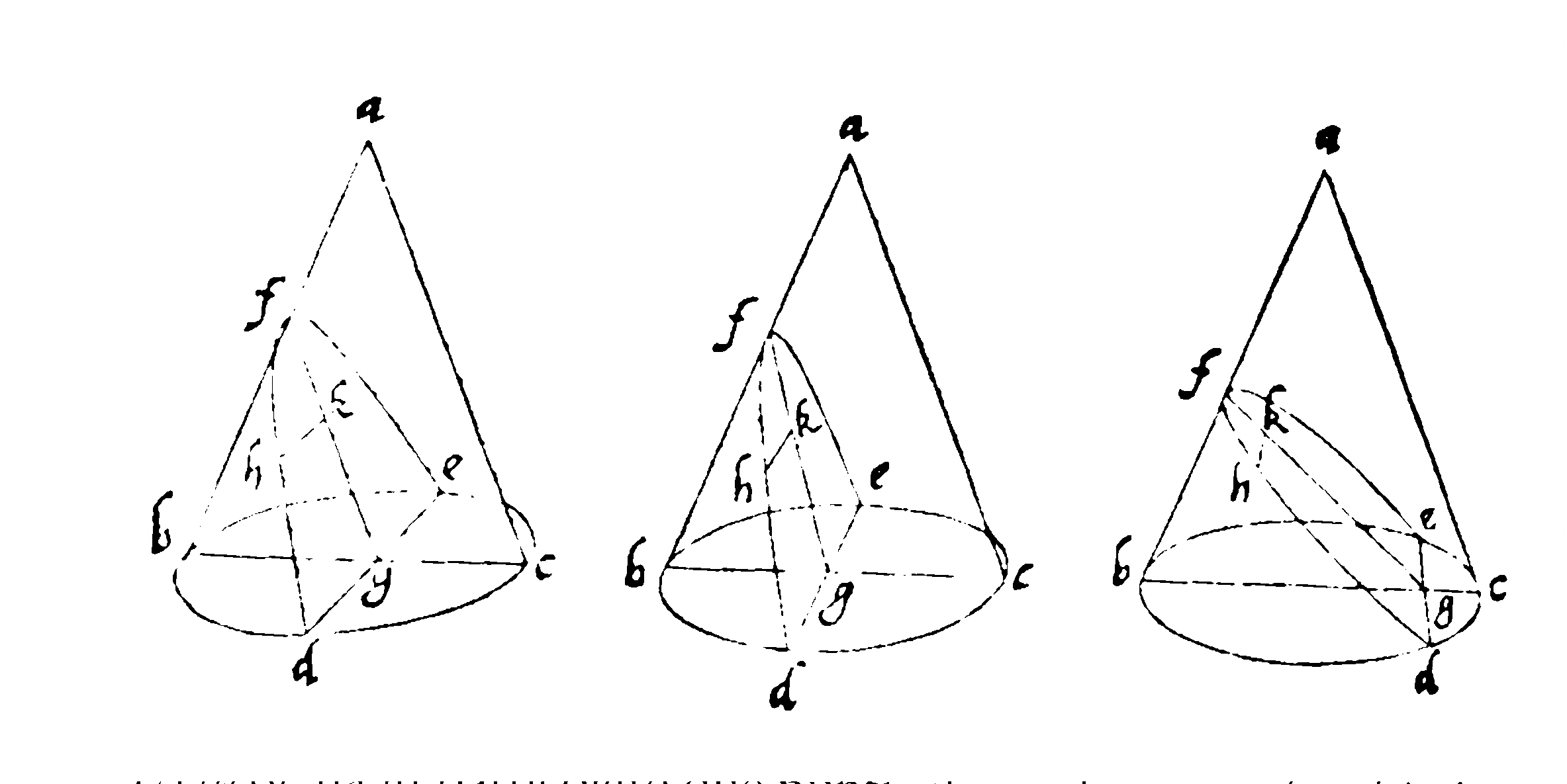Dobbiamo ad Apollonio di Perga (III-II sec. a. C.) lo studio più ampio che ci sia giunto dall'antichità, riguardante le sezioni coniche. Apollonio dimostra tra l'altro una serie di proprietà che condurranno a importanti applicazioni in molti campi della scienza e della tecnica.
L'ellisse ha in particolare due punti, che si chiamano fuochi, situati sul diametro maggiore, tali che la somma delle distanze dai fuochi è la stessa per qualunque punto sulla curva. Questo fatto può essere sfruttato per tracciare un'ellisse, in maniera alquanto approssimata ma sufficiente, ad esempio, per costruire delle aiuole a forma di ellisse (non a caso si chiama ellisse del giardiniere).
Una seconda proprietà dei fuochi consiste nel fatto che la perpendicolare all'ellisse in un suo punto qualsiasi divide per metà l'angolo formato dai segmenti che uniscono questo punto con i due fuochi. Di conseguenza, un raggio di luce che parte da uno dei fuochi, e si riflette sull'ellisse, passa per l'altro fuoco.
Lo stesso vale per le onde sonore: se si parla stando in un fuoco di una camera a volta ellittica, le onde sonore si rifletteranno sulla volta e andranno a concentrarsi di nuovo nell'altro fuoco.
Nel cerchio i fuochi cadono tutti e due nel centro; via via che l'ellisse si allunga, essi si allontanano sempre di più. La parabola non ha più che un solo fuoco: l'altro (per così dire) è andato all'infinito. I raggi che provengono da questo fuoco all'infinito sono delle rette parallele; riflettendosi sulla parabola vanno a finire nel fuoco rimasto.
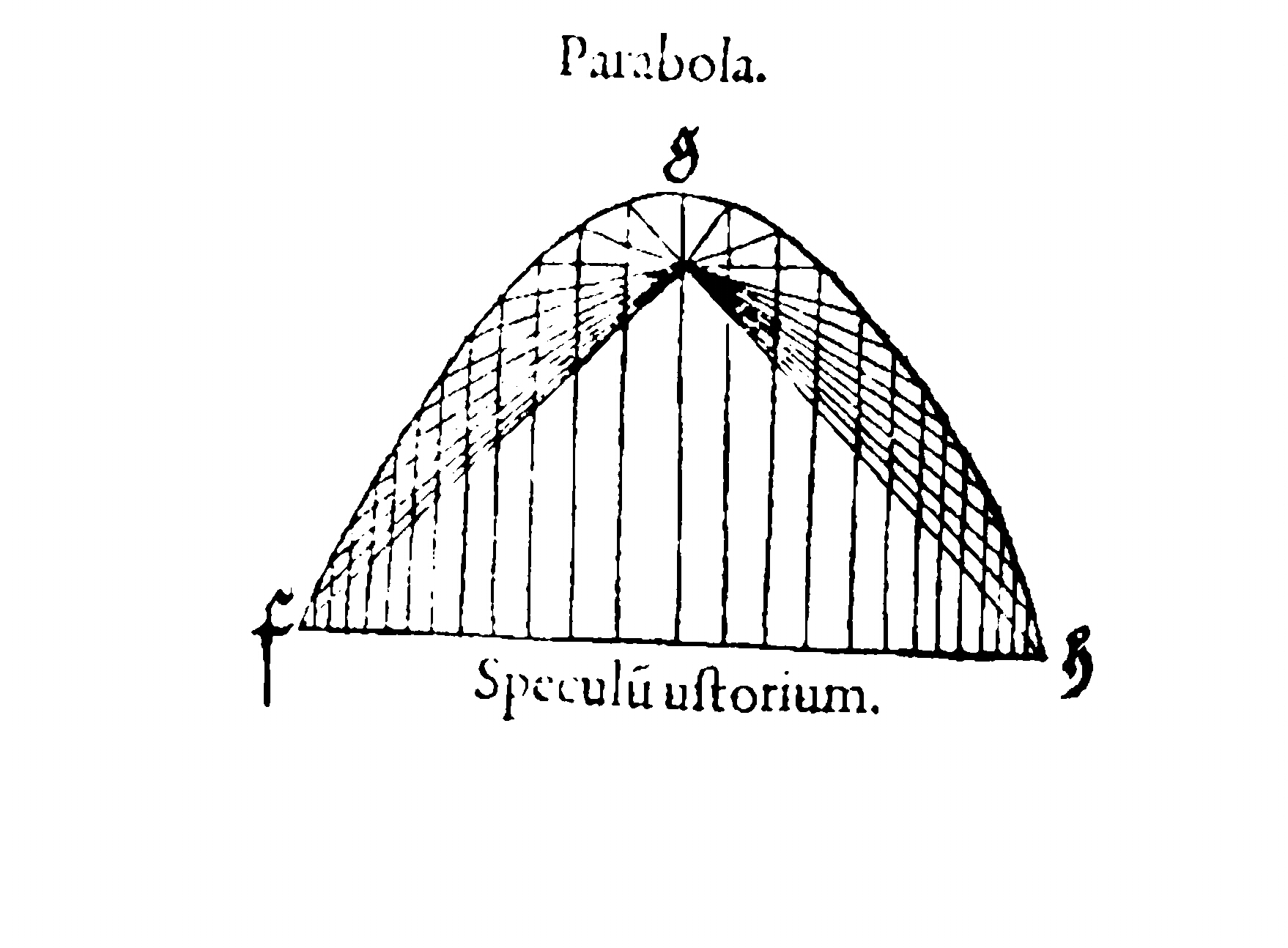
Se dunque vogliamo concentrare in un punto dei raggi paralleli (o praticamente paralleli, come ad esempio quelli del sole) si dovrà usare uno specchio a forma di parabola. Così facendo, si può costruire uno specchio ustorio, capace di incendiare un pezzo di carta o di legno posto nel fuoco. La leggenda, perché così si deve considerare, che Archimede (III sec. a. C.) avrebbe incendiato le navi romane con uno specchio ustorio, ha dato luogo a un numero considerevole di ricerche fino al seicento inoltrato.
I grandi radiotelescopi e le antenne paraboliche con le quali si ricevono le trasmissioni televisive dai satelliti agiscono secondo lo stesso principio: i segnali, praticamente paralleli data la grande distanza da cui provengono, rimbalzano sull'antenna e vengono concentrati sul ricevitore posto nel suo fuoco, aumentando così considerevolmente la potenza in ingresso. In altre parole, l'antenna parabolica funge da amplificatore, o meglio da condensatore dei segnali, altrimenti piuttosto deboli, provenienti dai satelliti.
Quello che succede con l'iperbole è un po' più complicato. Se ci mettiamo all'esterno, un raggio diretto verso un fuoco viene riflesso in direzione dell'altro fuoco. All'interno, un raggio che proviene da un fuoco, dopo una riflessione sull'iperbole sembra provenire dall'altro.
Precedente
Successiva
Se accendiamo una torcia elettrica, la luce della lampadina, uscendo dalla lente di forma circolare, formerà un cono di luce che ha come vertice il filamento della lampadina, e come asse la retta che passa per quest'ultimo e per il centro della lente. Supponiamo ora di dirigere il raggio luminoso verso una parete; la parte illuminata assumerà forme diverse, a seconda dell'inclinazione dell'asse, e precisamente: