The origins of geometry   

The first lines men ever imagined were straight lines and circles. These marked the birth of geometry, which means literally "Earth Measurement" giving us a precise idea of what these lines were meant for. The first geometry experts were land surveyors in Ancient Egypt. Greeks call them 'arpedonapti' -those who knot ropes. Egyptian experts used to tighten ropes on the land to mark lines and circles. Traces of this ancient usage are still present in many modern languages as, for example, in the saying "to draw a line". The employment of ropes for land measuring operations has remained unaltered for several centuries and can still be found in the work of land surveyors in relatively recent times.

Greek historians bear witness to the birth of geometry (literally: Earth Measurement) in Egypt. Herodotus says:

If the river had simply cancelled the borders of the piece of land, it was officials' role to redraw the exact divisions.

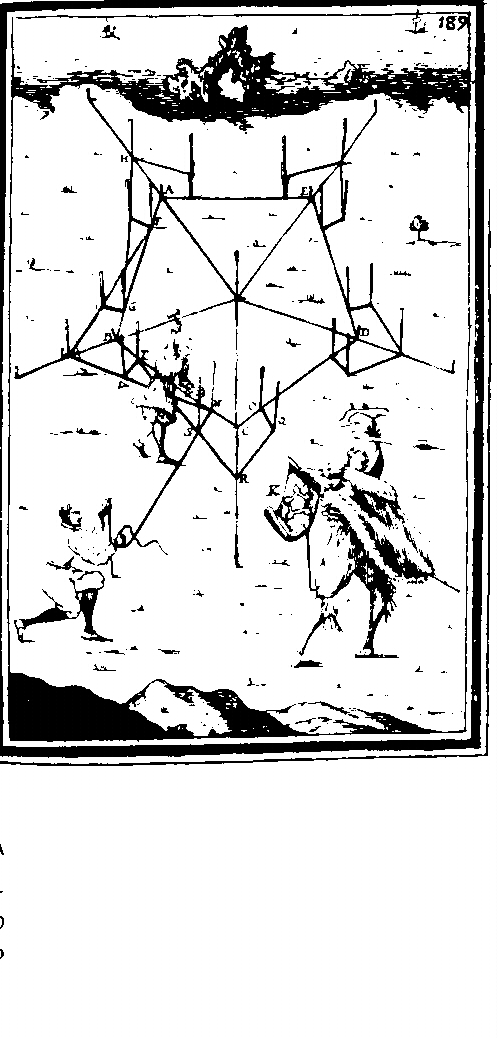Egyptian geometry experts were called "arpedonapti", those who knot ropes. It is by tightening ropes that they drew the two simplest and most important lines in geometry: the straight line and the circle. The first, simply tightening a rope between two points, a kind of operation which image is still present in the expressions "to draw a line", "to draw a perpendicular"; the second, making one of the two points turn around the other which is held fixed. Could they imagine the extent of the development of these two elementary practices? Most probably not. As a matter of fact the practical needs of ancient land measurers supposedly soon caused to emerge the necessity of works of the kind that today we call "with square and compass" and that should most properly be called "with circles and straight lines".

Nowadays, it is so natural to consider paper as the natural arena of geometry, so that we conceive the use of squares and compasses alone, as an arbitrary limit introduced by speculative spirits that preferred a few numbers of axioms to the multiple comforts deriving from the multiplicity of instruments. Consequently, the difference between the theoretical geometry expert -I am naturally referring to the classical, Euclidean one- and the technician -the one that takes measures, the architect- resides mainly in the fact that the first decides, voluntarily, not to use instruments, squares, and pantographs, that the second uses to his advantage.

This way, we tend to ignore completely geometry "in the field" in favor of that one "on paper", this failing to recognise that when we transfer geometrical operations from the field to paper, they will demand sometimes totally different techniques and methods.

One should not overlook the fact that the precision of a plan is far more necessary in the field (to the one that measures and divides into parts a piece of land, as well as to the architect that makes buildings -most often these two being the same person-) rather than on the paper. The architect that has a clear idea of the overall plan and that remembers the process he followed to get through it would need a draft. Relatively recent as well as old maps that were, inevitably, drawn with rudimentary instruments and supports, do not reproduce the borders of a piece of land exactly. In fact, this is impossible because even a mistake of a percentage point - the least that could occur in a reasonably large scale - would give birth to an absolute mistake that could hardly be accepted in the field. In this case, the knowledge of the form and the measures of the object that is to be described (a field, a building), are fundamental; it will be than up to the geometry expert to reproduce on the field the precision lacking on the paper. The same happens to the mathematician to whom the accuracy of figures are not at all useful in demonstrations. The geometry on paper substitutes the precision of the operations on the field, with the geometry of the mental process.

On the contrary, from logic to the material exactness, as a consequence of the necessary enlargement of scale to pass from the plan to the actual creation of it, the action of tightening a rope has remained one of the main operations since so far as Ancient Egypt and Ancient Greece. This practice has remained unaltered till modern times, passed only by the invention and improvement of certain optical instruments. While, on paper, it is quite easy to draw a perpendicular by means of rulers and squares, the same operation on the field, with the same degree of precision, demands radically different methods. In the field the square is useless because it is too small in relation to the dimensions of the forms. Even if the square is extremely precise, the perpendicular that it can draw will reach at its most more or less a meter. If we have to mark a square of 30 meters per side, we have to prolong this line 30 times. This would be such an inexact operation that it would probably result in the same results as if we measured the right angle roughly.

These reflections bring us back to the initial question: which techniques were used by Egyptian measurers to draw a square piece of land? How did they obtain a square angle?

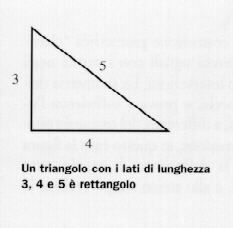
As some scholars have suggested, it is possible that they had the knowledge of Pythagoras' ( VI century B.C.) theorem or, more accurately, the consciousness of its opposite, that's to say the fact that a triangle with sides measuring 3, 4 and 5, in which the square on the longer side is equal to the sum of the squares on the other two sides, is a right angled triangle. Therefore, if we stretch a ring rope to a length of 12 units, marked at three points at a distance of 3, 4 and 5, towards the form of a triangle with the vertex in the marked points, the angle between the shortest sides of the triangle is a right angle.

It is not known if this was the process ancient land surveyors used in their time as has not been proven that ancient Egyptians knew that the triangle with sides 3, 4 and 5 is a right angled triangle. Even if they were aware of this, or of other Pythagorean triangles (as is strongly suggested by the presence of several Pythagorean trios, if not in Egyptian mathematics, then in the Babylonian), this necessarily implies that they knew the nature of, or at least how to create the right angle.

Where did this knowledge come from? Because of the lack of even partial documentation and witnesses, we can try to approach the problem from a different point of view, a mathematical rather than an historical one. The question we then have to pose is what makes a right angle different from the others? Or better, which is the peculiarity of the angle of the triangle with sides 3, 4 and 5?

The immediate answer is: unlike other triangles, Pythagorean ones and most particularly the simplest of them, the one with sides 3, 4 and 5, can be made to fit together turning them on one side and then again on the other. This way, a symmetrical configuration is obtained which totally fills up all the available space without overlapping or gaps.

No other angle but the right one has this symmetrical characteristic which becomes its own definition in the first complete book of geometry that ever reached our times, Euclid's Elements (IV century BC):

When a straight line falling on another one forms equal angles, these are both right ones.

The nature of the square angle resides in the fact that the angles resulting from the intersection of two straight lines are equal. This can be immediately demonstrated on paper by folding the paper along one of the converging lines and verifying that the other line folds on itself.

The "classical" geometrical construction which consists in marking two circles and then unifying their intersections also possesses this property. The symmetric character of the form is quite evident, and it's clear proof of the equality of the angles. Moreover, unlike the Pythagorean triangle which needs a further construction, in this case the form immediately suggests the definition of square angle through the equality of the angles and in the same time, constructs itself.

These are still simple suppositions. Without any doubt, this process is definitely simpler and of a greater precision than the former. One could say this way we can only mark the perpendicular which passes through the centre of the given segment, also called the axis of the segment. Nevertheless, it is not difficult to notice that if we need a perpendicular on one extreme, as in the case of drawing a square, it will be necessary to double the segment prolonging it towards where we want to draw the perpendicular and then to repeat the preceding process. It is necessary to observe that all these techniques are particularly suitable for flat land such as the Egyptian plain.